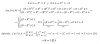Son subespacios: 1), 3), 4), 6), 7) , 9)

Observa que las expresiones de los trozos son continuas en todos sus puntos, y que solo es necesario estudiar la continuidad en el punto de corte: x = 1, según la definición:

1)

f(1) = -1² + 5(1) - 1 = -1 + 5 - 1 = 3;

2)

Límites laterales:

Lím(x→1-) f(x) = Lím(x→1-) (-x² + 5x -1) = 3,

Lím(x→1+) f(x) = Lím(x→1+) (2x + 1) = 3,

por lo que tienes:

Lím(x→1) f(x) = 3;

3)

Tienes que la función es continua en x = 1.

Luego, observa que las expresiones de los trozos son derivables en todos sus puntos, y que solo es necesario estudiar la dervabilidad en el punto de corte: x = 1, por medio de la definición:

f-' (1) = Lím(h→0-) [f(1+h) - f(1)]/h = 

= Lím(h→0-) [(-(1+h)²+5(1+h)-3) - 3]/h =

= Lím(h→0-) [1+2h+h² + 5+5h - 3 - 3]/h = 

= Lím(h→0-) [h² + 7h]/h = Lím(h→0-) h(h + 7)/h = Lím(h→0-) (h + 7) = 7,

f+' (1) = Lím(h→0-) [f(1+h) - f(1)]/h = 

= Lím(h→0-) [(2(1+h)+1) - 3]/h =

= Lím(h→0-) [2+2h+1 - 3]/h = 

= Lím(h→0-) [2h]/h = Lím(h→0-) 2 = 2,

luego, como las derivadas laterales no son iguales en el punto de corte, tienes que la función no es derivable en x = 1,

y la expresión de la función derivada queda:

f ' (x) =

-2x + 5                            si x < 1

no está definida           si  x = 1

2                                      si x > 1.

Espero haberte ayudado.

Observa que las expresiones de los trozos son continuas en todos sus puntos, y que solo es necesario estudiar la continuidad en el punto de corte: x = 1, según la definición:

1)

f(1) = -12 + a(1) - 1 = -1 + a - 1 = a-2;

2)

Límites laterales:

Lím(x→1-) f(x) = Lím(x→1-) (-x2 + ax -1) = a-2,

Lím(x→1+) f(x) = Lím(x→1+) (3x - b) = 3-b,

por lo que tienes que para que el límite exista debe cumplirse:

a-2 = 3-b, haces pasaje de término, y queda: a = 5 - b (1).

3)

Tienes que la función es continua en x = 1 con la condición señalada (1).

Luego, observa que las expresiones de los trozos son derivables en todos sus puntos, y que solo es necesario estudiar la dervabilidad en el punto de corte: x = 1, por medio de la definición:

f-' (1) = Lím(h→0-) [f(1+h) - f(1)]/h = 

= Lím(h→0-) [(-(1+h)2+a(1+h)-1) - (a-2)]/h =

= Lím(h→0-) [-1-2h-h2 + a+ah - 1 - a+2]/h = 

= Lím(h→0-) [-h2 - 2h + ah]/h = Lím(h→0-) h(h - 2 + a)/h = Lím(h→0-) (h - 2 + a) = -2 + a,

f+' (1) = Lím(h→0-) [f(1+h) - f(1)]/h = 

= Lím(h→0-) [(3(1+h)-b) - (a-2)]/h =

= Lím(h→0-) [3+3h-b - a+2]/h = 

= Lím(h→0-) [(5 - b) +3h - a]/h = sustituyes la expresión señalada (1) = 

= Lím(h→0-) [(5 - b) + 3h - (5 - b)]/h = Lím(h→0-) [3h]/h = 3,

luego, como las derivadas laterales deben ser iguales en el punto de corte, tienes que la función no es derivable en x = 1, solo si se cumple la condición: -2 + a = 3, haces pasaje de término, y queda: a = 5, 

y observa que el valor de la función para el punto de corte queda: f(1) = 5 - 2 = 3;

luego reemplazas en la expresión señalada (1), y queda: 5 = 5 - b, haces pasajes de términos, y queda:

b = 0;

luego, la expresión de la función queda:

f(x) =

-x² + 5x - 1                     si x < 1

3                                     si x = 1

3x                                   si x >1;

y la expresión de la función derivada queda:

f ' (x) =

-2x + 5                            si x < 1

3                                      si  x = 1

3                                      si x > 1.

Espero haberte ayudado.

Estos vídeos te ayudarán: 

Regla de la cadena

Te recomiendo que te aprendas la tabla de derivadas para funciones elementales, así como la regla de la cadena.

Sí, siempre. Y su dimensión es el número de grados de libertad( nº de parámetros) del sistema.

Razones trigonométricas

solo para guiarte, recuerda que en un triangulo rectangulo:

tg(a) =  cateto opuesto / cateto adyacente = -2/1

con eso hayas la "hipotenusa" , y ya puedes obtener las demas razones, pero teniendo en cuenta que sen(x) es positivo en el segundo cuadrante,  y cos(x) es negativo en el segundo cuadrante