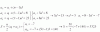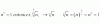-
María De Los Ángeles Mena
el 13/11/17 -
Daniel González
el 13/11/17Hola profe!Podria subir un video de como resolver una identidad por la piramide de Tartaglia?No se como se hace y mañana tengo examen
Ángel
el 13/11/17 -
Marest
el 13/11/17Me pueden ayudar por favor?
El ejercicio dice opera y simplifica:
1/2 • (5/3 − 7/10) − 3/4 • (3 − 1/5)
Gracias.
-
Vivi
el 13/11/17 -
Paco Acosta
el 13/11/17Estoy que no me entero...y este?
-
Paco Acosta
el 13/11/17 -
Francisco Arturo Tello Ulloa
el 13/11/17estava mirando con mi profeson de matematicas por que me hice una pregunta curiosa, el problema es que si se puede hacer esto: si n0=1 entonces, 1/0√n es pocible? ya buscamos por internet pero no encontramos algo hacerca de eso. apenas estamos viendo funciones cuadraticas y esas cosas en mi clase y me pregunte si la respuesta era 1 tambien.
-
Santiago Gamboa
el 13/11/17 -
beto rddz
el 13/11/17f(x) = (6X3 + 7X)4 (8x4 - 2x)6
hola !!
haber si por favor nos puede explicar como derivar esta por medio de la regla de la cadena.
gracias
Ángel
el 13/11/17f(x) = (6x3 + 7x)4 * (8x4 - 2x)6
Observa que es la función es:
1. un producto de funciones (la derivada es la derivada del primero por el segundo sin derivar más el primero sin derivar por el segundo derivado)
f´(x) = [(6x3 + 7x)4]´* (8x4 - 2x)6 + (6x3 + 7x)4 * [(8x4 - 2x)6]´
2. estas funciones están elevadas a potencias (para derivarlas se multiplica la función por el exponente y se eleva ésta a una unidad menos, a lo obtenido se le multiplica la derivada de la función)
[(6x3 + 7x)4]´= 4(6x3 + 7x)3*(18x2+7)
[(8x4 - 2x)6]´ = 6(8x4 - 2x)5*(32x3-2)
Entonces la derivada es:
f´(x) = 4(6x3 + 7x)3*(18x2+7)*(8x4 - 2x)6 + (6x3 + 7x)4 *6(8x4 - 2x)5*(32x3-2)
-
Santiago Gamboa
el 13/11/17
Hola, me podrían ayudar con esta? Estime el área debajo de la gráfica de f(x) = sin x desde 0 y π usando tres subintervalos y los puntos medios.
Antonius Benedictus
el 13/11/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Antonio Silvio Palmitano
el 13/11/17Puedes tomar los subintervalos:
I1 =[0,π/3], cuya longitud es: L1 = π/3 - 0 = π/3, cuyo punto medio es: x1 = π/6. y para él la función toma el valor: y1 = sen(π/6) = 1/2,
y el área para este subintervalo queda: A1 = L1*y1 = (π/3)*(1/2) = π/6;
I2 =[π/3,2π/3], cuya longitud es: L2 = 2π/3 - π/3 = π/3, cuyo punto medio es: x2 = π/2. y para él la función toma el valor: y2 = sen(π/2) = 1,
y el área para este subintervalo queda: A2 = L2*y2 = (π/3)*(1) = π/3;
I3 =[2π/3,π], cuya longitud es: L3 = π - 2π /3 = π/3, cuyo punto medio es: x3 = 5π/6. y para él la función toma el valor: y3 = sen(5π/6) = 1/2,
y el área para este subintervalo queda: A3 = L3*y3 = (π/3)*(1/2) = π/6.
Luego, tienes que la suma de las áreas correspondientes a los subintervalos es igual al área estimada bajo la curva, en el intervalo indicado en tu enunciado:
A = A1 + A2 + A3 = π/6 + π/3 + π/6 = π.
Observa que como hemos empleado muy pocos subintervalos, tenemos que la estimación del área no es buena.
Espero haberte ayudado.
