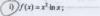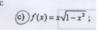-
Antonio Silvio Palmitano
el 13/11/17Plantea la expresión del incremento de la función:
Δf = f(x+h) - f(x) = (x+h)2ln(x+h) - x2lnx = (x2+2xh+h2)ln(x+h) - x2lnx = x2ln(x+h) + 2xhln(x+h) + h2ln(x+h) - x2lnx,
ordenas términos, agrupas términos, extraes factores comunes, y queda:
Δf = x2( ln(x+h) - lnx ) + h( 2xln(x+h) + hln(x+h) );
luego, divides en todos los términos de la ecuación por h, y queda:
Δf/h = x2( ln(x+h) - lnx )/h + ( 2xln(x+h) + hln(x+h) ),
luego, tomas límite que h tendiendo a cero en todos los términos de la ecuación, y queda:
f ' (x) = Lím(h→0) x2( ln(x+h) - lnx )/h + Lím(h→0) ( 2xln(x+h) + hln(x+h) ),
extraes factor común en el primer término, resuelves en el segundo término, y queda:
f ' (x) = x2Lím(h→0) ( ln(x+h) - lnx )/h + 2xlnx + 0,
luego, observa que la expresión remarcada corresponde a la expresión de la función derivada del logaritmo natural, sustituyes, y queda:
f ' (x) = x2(1/x) + 2xlnx + 0,
luego, simplificas en el primer término, cancelas el término nulo, y queda:
f ' (x) = x + 2xlnx.
Espero haberte ayudado.
-
Ángel
el 13/11/17No es correcto, el dominio es (-1,0) U (0,1)
Del dominio se deduce que está definida en (-1,1) y hay una discontinuidad en x=0
Para ver el proceso pincha en "mostrar pasos" en el apartado dominio en este enlace: https://es.symbolab.com/solver/step-by-step/f%5Cleft(x%5Cright)%3D%5Cfrac%7B1%7D%7Bx%7Dln%5Cleft(%5Cfrac%7B1%2Bx%7D%7B1-x%7D%5Cright)
-
Hola,
Por favor, necesitaría ayuda con este ejercicio sobre las rectas de una ecuación. Después de ver los vídeos he intentado hacerlo expresándolo de forma explícita y calculando la pendiente. Al estar planteado distinto, tengo dudas porque no sé si puedo despejar tanto x, como y. Muchas gracias!!
-
Hola buenas tardes me podrian ayudar con este problema por favor, gracias de antemano
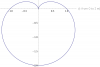
Calcular la longitud del arco dada la curva
r = 1-sent con [0,2pi]
-
Hola unicoos , una duda la regla de L'Hôpital solo se aplica cuando hay un indeterminación 0/0 o infinito/infinito???? Gracias!!