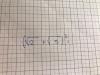-
Carlos
el 13/11/17como podría representar en R3 la ecuación x=y?
de manera numerica se podria hacer? porque en R2 la ecuación x=y viene de y= ax + b y como b= 0, corta en las coordenadas (0,0) y según aumenta x aumenta y siendo creciente pero en R3 no sabría como representarlo
-
Andreus Lopez Castro
el 13/11/17
alguien me podría ayudar con este ejercicio de razon de cambio?no se como plantearlo
Antonio Silvio Palmitano
el 13/11/17Plantea la velocidad angular de giro de la luz del faro:
ω = 2 rev/min = 2*2π/60 = π/15 rad/s.
Luego, plantea la definición de velocidad angular:
dθ/dt = ω, reemplazas el valor remarcado, y queda: dθ/dt = π/15 rad/s (1).
Luego, plantea en el triángulo rectángulo que tienes en tu imagen (expresamos las longitudes en metros):
y/1000 = tanθ, aquí haces pasaje de divisor como factor, y queda: y = 1000*tanθ (2).
Luego, plantea la expresión de la velocidad lineal:
v = dy/dt = 1000*(1/cos2θ)*(dθ/dt), reemplazas el valor señalado (1) y queda:
v = (200π/3)*(1/cos2θ) = (200π/3)*(tan2θ + 1) (3).
Luego, para un punto de la playa que se encuentra a 500 metros de distancia del punto ubicado frente al faro, tienes:
tanθ = 500/1000 = 1/2;
luego reemplazas en la expresión señalada (3), y tienes para la velocidad del rayo de luz sobre la playa en el punto indicado:
v = (200π/3)*(1/4 + 1) = (200π/3)*(5/4) = 250π/3 m/s ≅ 261,799 m/s.
Espero haberte ayudado.
-
Rubén
el 13/11/17Hola chicos, ¿podéis ayudarme con esta dudilla de mates? Es de un ejercicio donde te dan una sucesión de números y tienes que probar su veracidad mediante el método de inducción. A continuación adjuntaré la foto donde señalo en amarillo a lo que quiero llegar y en verde en el paso es el que me estanco y en el que no se que hacer más para llegar a lo que tengo en amarillo. ¿Pueden decurme que es ese algo que debo hacer para llegar a lo que está en amarillo desde lo que está señalado en verde por favor? Gracias de antemano y perdón por explicarme tan mal.
-
Sebastián
el 13/11/17hola. Me podrían ayudar a resolver este problema....
Una función F de dos variables está dada por la expresión z= F(x;y) y se considera F(x:y)=c esta ecuación corresponde a los puntos de la superficie que se obtienen seccionándola con el plano de ecuación z=c paralelo al plano coordenadas z=0. Para diferentes valores de “c” se obtienen distintas curvas que al proyectarlas sobre el plano xy forman una familia de curvas de nivel.
Si todas las curvas de nivel de la superficie dada por z= F(x:y) son rectas paralelas, ¿implica esto que la gráfica de z=F(x:y) es un plano?
Muchas Gracias
Antonio Silvio Palmitano
el 13/11/17Vamos con un contraejemplo.
Considera que la gráfica de la función tiene la expresión: z = ∛(x + y) (observa que no es la ecuación de un plano);
luego, plantea la expresión de la familia de las curvas de nivel (z = c), y queda:
∛(x + y) = c, haces pasaje de raíz como potencia, y queda:
x + y = c3, haces pasaje de término, y queda:
y = - x + c3,
que corresponde a una familia de rectas cuya pendiente es m = -1, y, por lo tanto, son todas rectas paralelas.
Observa que hemos visto que la familia de curvas de nivel está formada por rectas paralelas, pero la gráfica de la función no es un plano.
Espero haberte ayudado.
-
Its Gonza
el 13/11/17 -
Amaia Rodriguez
el 13/11/17No se por donde empezar esta ecuación:
x2+8/x2 - x-2/x2-3x
yo lo que hago es x*x2-3
pero me da mal
Neofito 007
el 13/11/17
Ángel
el 13/11/17Si te refieres a la ecuación:
(x2 +8)/x2 - (x -2)/x2 - 3x = 0
Pasamos a común denominador:
(x2 +8)/x2 - (x-2)/x2 - (3x3)/x2= 0
Sumamos/restamos los numeradores:
((x2 +8 - (x-2)-2-3x3))/x2=0
Pasamos multiplicando el x2:
((x2 +8 - (x-2)-2-3x3) =0*x2
Simplificamos:
x2 +8 - x+2-2-3x3= 0
y obtenemos el polinomio:
-3x3+x2 -x+8= 0
El valor aproximado por el método Newton-Raphson es x≈1.42 (no se puede solucionar por Ruffini, por lo que conviene que mandes el enunciado sin ambigüedades si no estás en la Universidad).
-
Antonio Fidalgo
el 13/11/17
Hola a todos. Tengo un problema de matrices y no tengo ni idea de como empezar a desarrollarlo. ¿Alguien me puede echar una mano?
Antonius Benedictus
el 13/11/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Rodrigo Ivan Saez
el 15/11/17el tema es de analisis estructural, asi que el primer punto, fisicamente hablando, no estoy seguro que significaran las columnas de D...
Pero el resto de puntos es aplicacion de la ecuacion matricial:
| y1|....| 0,005 0.002 0.001 |....| f1 |
| y2| = | 0,002 0.004 0.002 | X | f2 |
| y3 |...| 0.001 0.002 0.005 |....| f3 |
Y debes hallar la inversa de la matriz D para el ultimo.
El primer punto es reemplazar (f1,f2,f3) = (30,50,20) y hacer el producto de matrices para hallar (y1,y2,y3)
el ultimo punto es reemplazar (y1,y2,y3)=(0, 0.001 , 0.004) y hallar (f1,f2,f3), y para eso debes hallar la inversa de D, asi tendras la ecuacion matricial f = D^-1 * y (obviamente es analoga a la primera, pero la matriz es diferente
-
Francisco Gimenez
el 13/11/17 -
Diego Mauricio Heredia
el 13/11/17 -
DAVID
el 13/11/17De un número de tres cifras sabemos que su suma es 12, que la cifra de las unidades es igual a la semisuma de las cifras de las decenas y, por último, que el número que resulta al invertir las cifras del buscado es 198 unidades más pequeño que este. ¿De qué número se trata?
Antonio Silvio Palmitano
el 13/11/17Plantea el número buscado:
N = 100a + 10b + c (observa que a indica centena, b indica decena y c indica unidad).
Luego, tienes en tu enunciado:
a + b + c = 12 (1) (la suma de las cifras es doce);
c = (a + b)/2 (2) (la cifra de las unidades es la semisuma de las cifras de las decenas y las centenas),;
(100c+10b+a) = (100a+10b+c) - 198, eliminas agrupamientos, haces pasajes de términos, y queda:
99c - 99a = -198, divides por 99 en todos los términos de la ecuación, y queda:
c - a = - 2 (3).
Luego, sustituyes la expresión señalada (2) en las ecuaciones señaladas (1) (3), y queda el sistema:
a + b + (a + b)/2 = 12 (4),
(a + b)/2 - a = - 2 (5).
Luego, distribuyes y reduces términos semejantes en la ecuación señalada (4), y queda:
3(a + b)/2 = 12, aquí multiplicas en ambos miembros por 2/3, y queda: a + b = 8,
haces pasaje de término, y queda: b = 8 - a (6),
luego, distribuyes en el primer término de la ecuación señalada (5), reduces términos semejantes, y queda:
- a/2 + b/2 = - 2,
multiplicas en todos los términos de la ecuación por 2, y queda:
- a + b = - 4 (7);
luego, sustituyes la expresión señalada (6) en la ecuación señalada (7), y queda:
- 2a + 8 = - 4, haces pasaje de término, luego pasaje de factor como divisor, y queda: a = 6;
luego, reemplazas el valor remarcado en la ecuación señalada (6), y queda: b = 2;
luego, reemplazas los valores remarcados en la ecuación señalada (2), y queda: c = (6 + 2)/2 = 8/2 = 4.
Luego, tienes para el número de tres cifras planteado:
N = 100a + 10b + c = 600 + 20 + 4 = 624.
Espero haberte ayudado.
