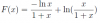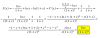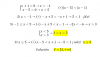-
Usuario eliminado
el 9/11/17 -
berni
el 9/11/17 -
Bárbara Acosta
el 9/11/17Hola David,
Tengo una duda, el otro día mi profesora me puso el siguiente problema:
Un banco ofrece un 12,5% anual de interes simple. Calcula cuánto tiempo debe pasar para que el capital se duplique.
Al momento un amigo y yo lo vimos claro, eran 8 años. La profe se sorprendió y le explicamos que era lógica que el doble de algo era el 100% entonces dividiendo 100:12,5 daba el resultado. Nos dijo que lo teniamos que hacer con la fórmula del interes simple ( Cf=Ci(1+(r:100)n) ) ya que de la otra forma no justificabamos la respuesta.. y que además no siempre podría funcionar.. pero no nos ha demostrado ningún ejemplo en el que se demuestre que no siempre vale. Mi duda es: ¿Hay alguna justificación para que siempre salga así?¿Algún razonamiento para justficar la respuesta sin tener que hacer la fórmula?
Muchas graciass,nos vemos en clases :) (me he dado cuenta de que tenía que ponerlo en la foro jaja)
Antonio Silvio Palmitano
el 10/11/17Puedes denominar C0 al capital inicial.
Luego de 1 año, tienes como capital: C1 = C0 + 0,125*C0 = C0*(1+0,125) = C0*1,125 = C0*1,1251.
Luego de 2 años, tienes como capital: C2 = C1 + C1*0,125 = C1*(1+0,125) = C1*1,125 = sustituyes = C0*1,125*1,125 = C0*1,1252.
Luego de 3 años, tienes como capital: C3 = C2 + C2*0,125 = C2*(1+0,125) = C2*1,125 = sustituyes = C0*1,1252*1,125 = C0*1,1253.
Luego, puedes inferir que luego de n años, tienes como capital: Cn = C0*1,125n.
Luego, puedes plantear para la cantidad de periodos de capitalización necesarios para duplicar el capital inicial:
Cn = 2*C0, sustituyes en el primer miembro, y queda:
C0*1,125n = 2*C0, haces pasaje de factor como divisor, y queda:
1,125n = 2, tomas logaritmos decimales en ambos miembros, y queda:
log(1,125n) = log(2), aplicas la propiedad del logaritmo de una potencia en el primer miembro, y queda:
n*log(1,125) = log(2), haces pasaje de factor como divisor, y queda:
n = log(2) / log(1,125), resuelves el segundo miembro, y queda:
n ≅ 5,884949,
por lo que puedes considerar que con seis periodos de capitalización, o sea: seis años, se duplica el capital inicial, y sobra una pequeña parte.
Espero haberte ayudado.
-
federico garcia
el 9/11/17 -
Juan
el 9/11/17
¿Cómo calculo el límite de esta sucesión? ¿Teorema sandwich?
Antonius Benedictus
el 10/11/17Rodrigo Ivan Saez
el 13/11/17miralo de esta forma: el termino mayor de la sumatoria es cuando k=1, este termino es a1, si sumamos a1+a1+a1... "n veces" (esta suma seria n*a1, por eso el "n" en el numerador), es claro que ésta suma sera mayor que la suma original.
lo mismo va para el otro caso caso, el termino menor de la sumatoria es cuando k=n, este es an, si sumamos an+an+... "n veces" (esta suma seria n*an), es tambien claro que ésta suma sera menor que la suma original
-
Meli
el 9/11/17hola, hay algún video de raices cúbicas?
Ángel
el 9/11/17 -
Raisa
el 9/11/17
Hola podríais ayudarme porfavor???????? es super urgente
David
el 15/11/17¿qué ejercicio? ¿los tres?...
Lo siento pero se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-) -
Raisa
el 9/11/17
Hola lo tengo que entregar hoy podéis ayudarme?
David
el 15/11/17Haz el determinante e iguala a 0...
Matrices
Echale un vistazo a los videos de ecuaciones matriciales...
A partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Carlos Artemio Mulas Saurí
el 9/11/17Hola, llevo ya un buen rato buscando vídeos sobre la forma matricial de un sistema de ecuaciones, si lo busco por el nombre no me sale nada (ha llegado a estar cargando 10-15min y nada) y probando otros métodos de búsqueda tampoco me ha salido nada... Cómo me puedo hacer con uno de esos vídeos? Sí que hay vídeos de ecuaciones matriciales, pero no encuentro vídeos sobre la forma matricial de un sistema de ecuaciones. Un saludo y gracias :)
-
Inés
el 9/11/17Hola, como se resuelve este problema? (Durante este tema hemos hecho Gauss, pero en este problema no se como resolverlo)
-En el pasado mes de enero, Juan, Carla y Laura invierten en bolsa. Carla invierte el doble que Laura. Aquél mes, Juan y Carla obtienen unos beneficios del 30%, y Laura perdidas del 10%. Pero obtienen conjuntamente unos beneficios del 20%. Volvieron a invertir en febrero, incrementando cada uno un 10% de sus inversiones iniciales. Si el mes de febrero invierten entre todos 770 euros, ¿que cantidad ha invertido cada uno en el mes de enero?
