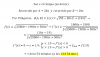Tienes la ecuación matricial:

2*A²*B^-1 = I,

planteas la igualdad entre los determinantes:

|2*A²*B^-1| = |I|,

luego, aplicas la propiedad del determinante de una matriz multiplicada por una constante (observa que el orden de las matrices es tres), y queda:

2³*|A²*B^-1| = |I|,

luego, aplicas la propiedad del determinante de un producto, y queda:

2³*|A²|*|B^-1| = |I|,

aplicas la propiedad del determinante de una potencia de una matriz, y queda:

2³*|A|²*|B^-1| = |I|,

aplicas la propiedad del determinante de la inversa de una matriz, y queda:

2³*|A|²*(1/|B|) = |I|,

reemplazas valores (recuerda que el determinante de la matriz identidad es igual a 1), y queda:

2³*|A|²*(1/2) = 1,

resuelves el producto numérico en el primer miembro, y queda:

4*|A|² = 1,

haces pasaje de factor como divisor, y queda:

|A|² = 1/4,

haces pasaje de potencia como raíz, y queda:

|A| = -1/2 o |A| = 1/2.

Espero haberte ayudado.

Tienes los datos:

centro de simetría: C(0,0);

vértice secundario: B₁(-3,0), por lo que tienes su simétrico: B₂(3,0);

vértice principal: A₁(0,a), y su simétrico A₂(0,-a);

foco: F₁(0,4), y su simétrico F₂(0,-4).

Luego, observa que la distancia entre el centro y un vértice secundario es: b = 3.

Luego, observa que la distancia entre el centro y un foco es: c = 4.

Luego, plantea la relación entre semiejes:

a² = b² + c², reemplazas y queda:

a² = 3² + 4² = 9 + 16 = 25, luego, calculas su raíz cuadrada y queda: a = 5,

que es la distancia entre el centro y cada uno de los vértices principales: A₁(0,5) y A₂(0,-5).

Luego, plantea la ecuación cartesiana de la elipse con centro en el origen de coordenadas, y eje focal OY:

x2/b2 + y2/a2 = 1,

reemplazas valores en los denominadores, los resuelves, y queda:

x²/9 + y²/25 = 1.

Espero haberte ayudado.

 ln a2 + ln b2=

2*ln a + 2*ln b=

2*3 + 2*5=

6 + 10=

16

Observa que el dominio de la función es R, ya que el argumento del logaritmo es estrictamente positivo, y observa que para x tendiendo a +infinito y a -infinito, tienes que la función tiende a +infinito.

Luego, plantea la expresión de la función derivada primera:

f ' (x) = 2x/(x²+1),

luego, plantea la condición de punto crítico (posible máximo o posible mínimo):

f ' (x) = 0, sustituyes y queda:

2x/(x²+1) = 0, haces pasaje de divisor como factor (observa que el denominador es estrictamente positivo), y queda:

2x = 0, haces pasaje de factor como divisor, y queda: x = 0,

luego, evalúas para dos valores, uno menor y otro mayor que cero, y tienes:

f ' (-1) = -2/2 = - 1 < 0, por lo que tienes que la gráfica de la función es decreciente en el intervalo: (-∞,0),

f(1) = 2/2 = 1 > 0, por lo que tienes que la gráfica de la función es creciente en el intervalo: (0,+∞);

por lo tanto, tienes que la gráfica de la función presenta un mínimo en x = 0, y el valor dela función para él es: f(0) = 0.

Luego, plantea la expresión de la función derivada segunda:

f ' ' (x) = ( 2(x²+1) - 2x(2x) ) / (x²+1)² = (2 - 2x²) / (x²+1)² = 2(1 - x²) / (x²+1)²,

luego, plantea la condición de posible punto de inflexión:

f ' ' (x) = 0, sustituyes y queda:

2(1 - x²) / (x²+1)² = 0, haces pasaje de divisor como factor (observa que el denominador es estrictamente positivo), y queda:

2(1 - x²) = 0, haces pasaje de factor como divisor, y queda:

1 - x² = 0, haces pasaje de término, y queda:

-x² = -1, multiplicas por -1 en ambos miembros, luego haces pasaje de potencia como raíz, y tienes dos opciones:

x = -1 o x = 1;

luego, evalúas para tres valores, uno menor que -1, uno intermedio entre -1 y 1, y otro mayor que 1,y tienes:

f ' ' (-2) = -6/25 < 0, por lo que tienes que la gráfica de la función es cóncava hacia abajo en el intervalo: (-∞,-1),

f ' ' (0) = 2/1 = 2 > 0, por lo que tienes que la gráfica de la función es cóncava hacia arriba en el intervalo: (-1,1),

f ' ' (2) = -6/25 < 0, por lo que tienes que la gráfica de la función es cóncava hacia abajo en el intervalo: (1,+∞,-1);

luego, tienes que la gráfica de la función presenta inflexiones en: x = -1, y el valor de la función para él es: f(-1) = ln(2), y en x = 1, y el valor de la función para él es: f(1) = ln(2).

Espero haberte ayudado.

No se entiende bien lo que pides...si eres de bachillerato manda el enunciado con el que tengas problema y te explicamos.

Integrales definidas y área bajo una curva

Pero no te dan las funciones que representan esas curvas ?? , de lo contrario si sólo es la gráfica  se tiene que calcular las funciones , hay infinitas posibilidades aunque se puede suponer lo más elemental aún así es trabajoso.
Debes poner el ejercicio completo con su respectivo enunciado .

Mejor que pongas el límite de esta forma:

lim(x→0⁺)  1÷[1+(1/x)^1/x] =

[lim(x→0⁺) 1] ÷ [lim(x→0⁺) 1+(1/x)^1/x] =

1÷∞ =

0

Tiene que ser por L'hopital 

¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).