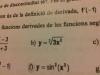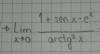-
Eric
el 6/11/17Te recomiendo que te mires las propiedades.
Aún así visita esta calculadora (tiene de todo: geometría, trigonometría, álgebra y demás) : https://es.symbolab.com/solver/derivative-calculator Te viene paso a paso. Por cierto, IMPORTANTE: donde el recuadro para introducir la derivada no pongas "y=", pon directamente lo de después del igual. ¡Un saludo!
-
Antonius Benedictus
el 6/11/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Antonio Silvio Palmitano
el 6/11/17Observa que tienes un sistema de dos ecuaciones lineales de primer grado, homogéneo y con tres incógnitas, por lo que tienes que el sistema es compatible indeterminado y admite infinitas soluciones.
Luego, mantienes la primera ecuación, a la segunda le sumas la primera, y queda:
4x - 2y - z = 0
7x - 6y = 0, aquí haces pasaje de término, y queda: -6y = -7x, haces pasaje de factor como divisor, y queda: y = (7/6)x,
luego, sustituyes en la primera ecuación, y queda:
4x - (7/3/x - z = 0, reduces términos semejantes, y queda:
(5/3)x - z = 0, aquí haces pasaje de término, y queda: (5/3)x = z;
luego, el sistema tiene infinitas soluciones, que quedan expresadas:
x ∈ R, y = (7/6)x, z = (5/3)x.
Espero haberte ayudado.
-
1) como puedo resolver el sig ejercicio de distribucion binomial negativa. me dio un resultado de 0.0000451584 no se si sea correcto saludos.
En una cadena de montaje de repuestos para automóviles se fabrica un 2% de piezas defectuosas. Se envía un lote de 500 piezas a un taller. Calcular la probabilidad de que en una muestra de 10 piezas elegidas al azar se encuentre dos o más defectuosas.Antonio Silvio Palmitano
el 6/11/17Tienes la variable aleatoria con distribución binomial:
X: "cantidad de piezas defectuosas en el lote",
cuyos parámetros son: n = 500, p = 0,02,
y la probabilidad complementaria queda: q = 0,98.
Luego, plantea:
p(X ≥ 2) = 1 - p(X < 2) = 1 - ( p(X = 0) + p(X = 1) ) (1).
Luego, planteas y calculas:
p(X = 0) = C(500,0)*0,020*0,98500 = 1*1*0,98500 ≅ 0,000041024,
p(X = 0) = C(500,1)*0,021*0,98499 = 500*0,02*0,98499 ≅ 0,000418612.
Luego reemplazas los valores calculados en la expresión señalada (1), y queda:
p(X ≥ 2) ≅ 1 - (0,000041024 + 0,000418612) = 1 - 0,000459636 = 0,999540364.
Espero haberte ayudado.
-
Saludos tengo duda con el siguiente enunciado: Distribucion binomial negativa.
1) La probabilidad de que un jugador de football marque un penalti es 0.4.suponiendo que los resultados de los lanzamientos son independientes y que la probabilidad de marcar se mantiene constante en cada lanzamiento, calcular la probabilidad de que este jugador tenga que lanzar x penaltis para marcar 3 goles.
Siento que al enunciado le hace falta datos para poder resolverlo, acaso estara mal formulado?
s
Antonio Silvio Palmitano
el 6/11/17Señalamos con G si el penalti termina en gol, y señalamos con X si no convierte gol.
Definimos la variable aleatoria: X = "cantidad de penaltis necesarios para convertir tres goles"
Luego, los primeros casos posibles son (observa que el último penalti debe ser convertido en gol, por lo que contamos cuántos casos tenemos para ubicar los dos primeros penaltis para convertir, y el resto para no convertir):
X = 3 (GGG),
observa que eliges dos penaltis para convertir entre dos posibles,
con probabilidad: 0,43 = C(2,2)*0,43*0,60 = 1*0,43*0,60,
X = 4 (XGGG, GXGG, GGXG),
observa que eliges dos penaltis para convertir entre tres posibles,
con probabilidad: C(3,2)*0,43*0,61 = 3*0,43*0,61,
X = 5 (XXGGG, XGXGG, XGGXG, GXXGG, GXGXG, GXGXXG),
observa que eliges dos penaltis para convertir entre cuatro posibles,
con probabilidad: C(4,2)*0,43*0,62 = 6*0,43*0,62,
X = 6 (XXXGGG, XXGXGG, XXGGXG, XGXXGG, XGXGXG, XGGXXG, GXXXGG, GXXGXG, GXGXXG, GGXXXG),
observa que eliges dos penaltis para convertir entre cinco posibles,
con probabilidad: C(5,2)*0,43*0,63 = 10*0,43*0,63,
X = 7 (XXXXGGG, XXXGXGG, XXXGGXG, XXGXXGG, XXGXGXG, XXGGXXG, XGXXXGG, XGXXGXG, XGXGXXG, XGGXXXG, GGXXXXG, GXGXXXG, GXXGXXG, GXXXGXG, GXXXXGG)
observa que eliges dos penaltis para convertir entre seis posibles,
con probabilidad: C(6,2)*0,43*0,64 = 15*0,43*0,64;
luego, puedes inferir la expresión de la distribución de probabilidad:
p(X = k) = C(k-1,2)*0,43*0,6k-3, con k ∈ N, k ≥ 3.
Espero haberte ayudado.
-
hola tengo una duda no se si me pueden ayudar...
Tengo una función de utilidades de una empresa, la función está en base al número de artículos que producen. Estoy haciendo un análisis marginal de las utilidades de la empresa, por lo que tengo que derivar la función, sin embargo al derivar la función esta no me queda en función de x para reemplazar el numero de artículos, sino que queda un número fijo, es decir en lugar de quedar U(X)= 0.1X-2, LO que me queda es U(x)= 2.4 (solo es un ejemplo)... esto que significa? que no importa el número de artículos la utilidad será constante o que?
Antonius Benedictus
el 6/11/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
hola, me podeis ayudar con este limite, preferiblemente resolverlo como limite infinitésimo por favor.
Antonio Silvio Palmitano
el 6/11/17Tienes que aplicar la Regla de L'Hôpital (recuerda que debes derivar al numerador (N) y al denominador (D) por separado), aplicas, y queda:
N ' = cosx - ex (observa que tiende a cero),
D ' = 2arctanx/(1+x2) (observa que tiende a cero),
luego, resuelves el cociente entre ambas expresiones, y el límite queda:
Lím(x→0) (cosx - ex)*(1+x2) / 2arctanx = Lím(x→0) (cosx + x2*cosx - ex - x2*ex) / 2arctanx;
luego, vuelves a aplicar la Regla de L'Hôpital (recuerda que vuelves a derivar por separado al numerador (N1) y al denominador (D1) de la expresión anterior:
N1' = -senx + 2x*cosx - x2*senx - ex - 2x*ex - x2*ex (observa que tiende a -1),
D1' = 2/(1+x2) (observa que tiende a 2),
luego tienes que el límite queda:
Lím(x→0) (-senx + 2x*cosx - x2*senx - ex - 2x*ex - x2*ex) / ( 2/(1+x2) ) = -1/2.
Espero haberte ayudado.
-
 amigos que tal por favor asesoramiento en este ejericicio de probabilidad de distribuciones binomiales y gracias de antemano
amigos que tal por favor asesoramiento en este ejericicio de probabilidad de distribuciones binomiales y gracias de antemanoAntonio Silvio Palmitano
el 6/11/17Tienes una distribución binomial, cuyos parámetros son: n = 15 (cantidad de ciudadanos), p = 0,3, y la probabilidad complementaria es: q = 1-p = 0,7.
Luego, te piden calcular:
p(x ≥ 5) = 1 - p(X < 5) = 1 - ( p(X = 0) + p(X = 1) + p(X = 2) + p(X = 3) + p(X =4) ) (1).
Luego puedes calcular:
p(X = 0) = C(15,0)*0,30*0,715 = 1*1*0,715 ≅ 0,004747562,
p(X = 1) = C(15,1)*0,31*0,714 = 15*0,3*0,714 ≅ 0,030520038,
p(X = 2) = C(15,2)*0,32*0,713 = 105*0,09*0,713 ≅ 0,091560115,
p(X = 3) = C(15,3)*0,33*0,712 = 455*0,027*0,712 ≅ 0,170040213,
p(X = 4) = C(15,4)*0,34*0,711 = 1365*0,0081*0,711 ≅ 0,218623131;
y solo queda reemplazar resultados en la expresión señalada (1), y resolver.
Espero haberte ayudado.
-