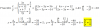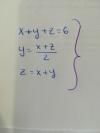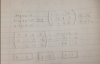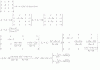-
Como resuelvo la siguiente ecuación: 6.271.755 = 20.000.000 * (0,7x) - .000.000 * (0,7x+3)
Ángel
el 5/11/17Lucia Quaglia
el 5/11/17Ángel
el 5/11/176.271.755 = 20.000.000 * (0,7x) - 5.000.000 * (0,7x *0.73)
6.271.755/5.000.000 = 20.000.000/5.000.000 * (0,7x) - 5.000.000/5.000.000 * (0,7x *0.73)
1,254351 = 4* (0,7x) - 1* (0,7x *0.73)
1,254351 = 4* (0,7x) - 1* (0,7x *0,343)
1,254351 = 4(0,7x) - 0,343(0,7x)
1,254351 = 3,657(0,7x)
0,7x= 1,254351/(3,657)
0,7x= 0,343
0,7x=0,73
x=3
-
Antonius Benedictus
el 5/11/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Como se resuelve este ejercicio? (Creo que debería de ser por el método de Gauss)
Dos familias van a una cafetería. La primera familia toma 1 refresco, 3, cafes y 7 magdalenas y paga 11.75€. La segunda familia pide 1 refresco, 4 cafes y 10 magdalenas y paga 15.5€.
Cuanto paga una familia que tome un refresco, un café y una magdalena? (Solución: 4.25€)
Lucía
el 5/11/17x+3y+7z = 11'75
x+4y+10z = 15'5
x+y+z = ?
Se me ocurre que puedes despejar x en la primera ecuación, por lo que te quedaría: x = 11'75-3y-7z entonces lo dejas todo en función de y y de z
(11'75-3y-7z)+3y+7z = 11'75
(11'75-3y-7z)+4y+10z = 15'5
luego sigues operando... es sólo una idea, a ver si te sirve!!
Antonio Silvio Palmitano
el 5/11/17Puedes llamar m a la suma abonada por la tercera familia.
Luego, mantienes la primera ecuación, a la segunda le restas la primera, y a la tercera le restas la primera, y queda:
x + 3y + 7z = 11,75
y + 3z = 3,75
-2y - 6z = m - 11,75.
Luego, mantienes las dos primeras ecuaciones, a la tercera le sumas el doble de la segunda, y queda:
x + 3y + 7z = 11,75
y + 3z = 3,75
0 = m - 4,25, aquí haces pasaje de término, y queda: 4,25 euros = m.
Espero haberte ayudado.
-
Lucía
el 5/11/17Primero ordena todo para que te quede así:
x+y+z = 6
x-2y+z = 0
x+y-z = 0
y luego usas el método de Gauss! Lo puedes encontrar en los vídeos del profe: https://www.unicoos.com/video/matematicas/2-bachiller/sistemas-de-ecuaciones/metodo-de-gauss/discutir-un-sistema-metodo-de-gauss
¡Un saludo :P!
Armando Fiorini
el 5/11/17
Ángel
el 5/11/17 -
-
Hola ,estoy resolviendo este ejercicio:
Un albañil que trabaja 8 horas diarias, tarda 5 días en solar 260m², ¿cuántos días tardara en solar un suelo de 500m² si trabaja 11 horas diarias?
La solución se que es 7 Días. pero tengo que resolver por proporcionalidad compuesta de magnitudes ,me he atascado y no consigo resolver. Gracias
Antonius Benedictus
el 5/11/17Neofito 007
el 5/11/17(Horas Diarias ) y (Días) son inversamente proporcionales ya que si trabajan más horas diarias menos días demoran .
(Días) y (Obra) son directamente proporcionales ya que a más días trabajando se realiza mayor obra.
De esto se obtiene :
(Horas diarias) * (Días) / (Obra) = constante
Bastaría reemplazar .
8*5 / 260 = 11*x /500 ==> x = 6.993 días , que es aproximadamente 7 días -
Alguna idea de cómo se hace esto?, es parte de una práctica de álgebra y no tengo muy claro el cómo plantearlo, se supone que debo hacerlo por gauss
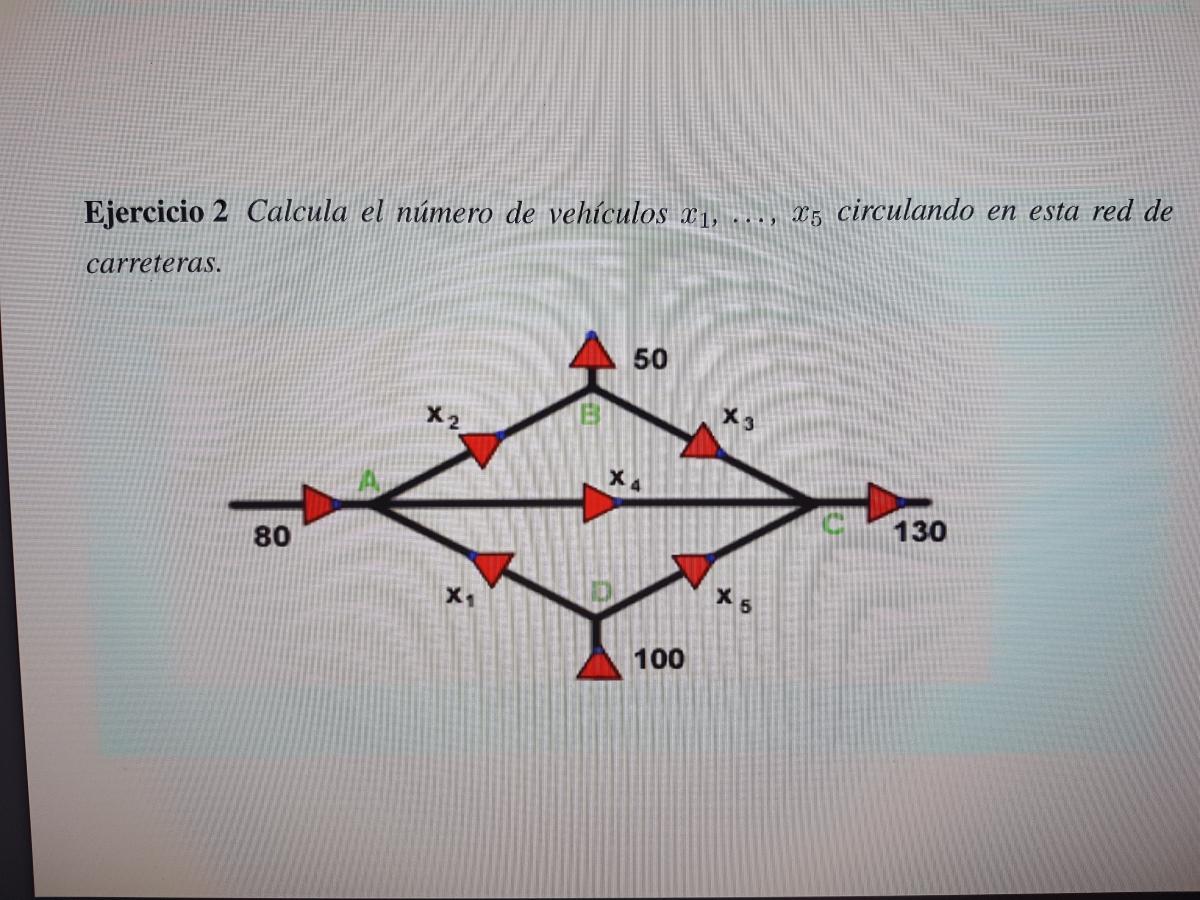
Ángel
el 5/11/17Jose L.
el 5/11/17 -
Hola, cómo se resuelve este ejercicio:
Los puntos A(0,3) y C(-2,-1), son vértices opuestos de un rectángulo, ABCD. Sabiendo que B está en el eje de abscisas, calcula las coordenadas de B y D.
El test ejercicio me mediante vectores perpendiculares, paralelos y con el mismo módulo y me da distintas soluciones. Cómo se resolvería esperamos?