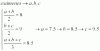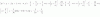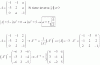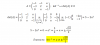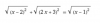-
Raisa
el 5/11/17podríais ayudarme?
Actividad 9
Miriam ha realizado tres exámenes de matemáticas y la nota media de los tres ha sido 8,5. Si la nota media de los dos primeros es 8, y la nota media de los dos últimos es 9
a) Plantea un sistema de ecuaciones lineales para halla la calificación de cada uno de los exámenes.
b) Resuelve, mediante el método de Gauss, el sistema planteado en el apartado anterior. -
Lsslie
el 5/11/17Hola! Me ayudan con una duda porfa?? Se trata de un ejericio de sistemas de ecuaciones, en este sistema en el apartado b) para resolver las soluciones de cada incógnita solo ha cogido las dos primeras ecuaciones poniendo z=landa, porque la tercera ecuacion no? Gracias!
x + y + kz = 6
x + ky + z= 0
kx - y + z = -6
Antonio Silvio Palmitano
el 5/11/17Observa que si reemplazas k = -1, tienes que la tercera ecuación es igual a la primera ecuación multiplicada por -1, por lo que tienes que la tercera ecuación es múltiplo de la primera, y puedes continuar la resolución del problema con las dos primeras ecuaciones (o podrías hacerlo también con las dos últimas).
Observa que reemplazas k = -1, y el sistema queda:
x + y - z = 6
x - y + z = 0
-x - y + z = -6
A la segunda ecuación le sumas la primera, a la tercera ecuación le sumas la primera, y queda.
x + y - z = 6
2x = 6
0 = 0, aquí tienes una identidad verdadera, por lo que debes continuar con las dos primeras ecuaciones.
Espero haberte ayudado.
-
AZUCENA
el 5/11/17En un diagrama de cajas y bigotes puede no haber un valor atípico?
-
alex
el 5/11/17Me podrían ayudar con la siguiente pregunta? Dice asi:
"Una poblacion x(t) crece con tiempo en acorde con dx/dt = (x - 1)(2x - 1). Sabiendo que x(0) = 0, cuánto tiempo tarda en llegar al 50% de su valor final?"
Supongo que el "valor final" al que se refiere la pregunta es el valor límite de la poblacion cuando el tiempo tiende a infinito.
Alguien podria hacerlo para ver que les da? A mi me dio tiempo = ln(1.5) pero no estoy seguro si esta correcto.
Muchas gracias!
Antonio Silvio Palmitano
el 5/11/17Separas variables en la ecuación diferencial, y queda:
( 1 / (x-1)(2x-1) )*dx = dt,
expresas la fracción algebraica del primer miembro como suma de fracciones parciales (te dejo la tarea), y queda:
( 1/(x-1) - 2/(2x-1) )*dx = dt,
integras en ambos miembros, y queda:
ln|x-1| - ln|2x-1| = t + C,
que es la solución general de la ecuación diferencial,
luego, reemplazas los valores de la condición inicial (t = 0, x = 0), cancelas términos nulos, y queda: C = 0,
luego, reemplazas en la expresión de la solución general, y queda:
ln|x-1| - ln|2x-1| = t,
que es la solución particular de la ecuación diferencial para la condición inicial de tu enunciado;
luego, aplicas la propiedad del logaritmo de una división en el primer miembro, y queda:
ln|(x-1)/(2x-1)| = t,
luego, multiplicas en ambos miembros por -1, y queda:
-ln|(2x-1)/(x-1)| = -1,
luego, aplicas la propiedad del logaritmo del recíproco de un argumento en el primer miembro, y queda:
ln|(2x-1)/(x-1)| = -1,
luego, compones en ambos miembros con la función inversa del logaritmo natural, y queda:
(2x-1)/(x-1) = e-t,
luego, haces la división entre polinomios en el primer miembro (observa que el cociente es 2, y que el resto es 1), y queda:
2 + 1/(x-1) = e-t,
luego, haces pasaje de término, y queda:
1/(x-1) = e-t - 2,
luego, haces pasaje de divisor como factor, y queda:
1 = (e-t - 2)(x-1),
luego, haces pasaje de factor como divisor, y queda:
1/(e-t - 2) = x - 1,
haces pasaje de término, y queda:
1/(e-t - 2) + 1 = x (1),
que es la expresión explícita de la ecuación diferencial de tu enunciado.
Luego, para estimar el valor final, planteas:
Lím(t→+∞) x(t) = Lím(t→+∞) (1/(e-t - 2) + 1) = 1/(0-2) + 1 = -1/2 + 1 = 1/2 = xf.
Luego, tienes para estudiar el valor de la función: x1 = (50/100)xf = 50/100)(1/2) = 1/4,
luego reemplazas en la ecuación señalada (1), y queda:
1/(e-t - 2) + 1 = 1/4,
luego, haces pasaje de término, y queda:
1/(e-t - 2) = -3/4,
luego, haces pasajes de divisores como factores, y queda:
4 = -3(e-t - 2),
luego, divides en ambos miembros de la ecuación por 1/3, distribuyes en el segundo miembro, y queda:
4/3 = -e-t + 2,
luego, haces pasajes de términos, y queda:
e-t = 2/3,
luego, compones en ambos miembros con la función inversa del logaritmo natural, y queda:
-t = ln(2/3),
multiplicas en ambos miembros por -1, aplicas la propiedad del logaritmo del recíproco del argumento en el segundo miembro, y queda:
t = -ln(2/3) = ln(3/2) = ln(1,5),
que es la respuesta que has consignado.
Espero haberte ayudado.
-
Daniel Domínguez
el 5/11/17Buenas, tengo que pasar esta ecuación: 3y2 + x + 5y + 1 =0, a la forma canónica de una parábola ( y - β )2 = 2p ( x - α ). He llegado hasta este punto ( y + 5/6 )2 = 13/36 -x/3, pero ahora no tengo muy claro como hallar 2p ( x - α ). Gracias
-
Paula Sánchez
el 5/11/17 -
Usuario eliminado
el 5/11/17 -
Rubén
el 5/11/17Hola, ¿me podrían decir el significado de esto? sen: [0, 2π]--> IR
¿Significa que es una función seno que está definida entre 0 y π?
-
Pilar Bravo Benítez
el 5/11/17Estoy intentando hallar los puntos de corte con el eje x de una función que expreso a continuación. Pare ello la igualo a cero. x^2-e^(-x^2)=0. Aplicando las reglas de los logaritmos y tal simplifico pero, no soy capaz de pasar de x2+2lnx2 = 0. Por tanteo he encontrado los puntos de corte con el eje x, que son +/-0,753. ¿Cómo puedo resolver esa ecuación sin recurrir al tanteo? Gracias por vuestra inestimable ayuda
Antonio Silvio Palmitano
el 5/11/17Has planteado la ecuación:
x2 - e-x^2 = 0,
luego, aplicas la sustitución (cambio de incógnita):
w = x2 (observa que w toma valores positivos), sustituyes, y queda:
w - e-w = 0, haces pasaje de término, y queda:
w = e-w, aplicas la propiedad de las potencias con exponente negativo en el segundo miembro, y queda:
w = 1/ew, haces pasaje de divisor como factor, y queda:
w*ew = 1, sustituyes la expresión de w, y queda:
x2*ex^2 = 1,
que es una ecuación trascendente, que no se puede resolver con métodos algebraicos elementales, por lo que debes recurrir a métodos de estimación,
y los valores que has consignado son muy buenas aproximaciones para la solución de la ecuación.
Espero haberte ayudado.
-
Isabel Lozano
el 5/11/17¿Cómo se resuelve una ecuación con tres factores de valor absoluto?
Ej: l(x-2)l+l(2x+3)l=l(x-1)l. hacerlo sin dividir la recta real en intervalos delimitados por los valores que hacen cero cada término de la ecuación; y después, trabajar cada intervalo de modo independiente al resto.
Es una duda de una alumna de 1º de Bachillerato.
Gracias
