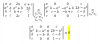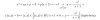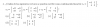-
hola me podriais ayudar con este problema de probabilidad por favor
Sabiendo que los sucesos A y B son incompatibles y con probabilidades P[A]≠0, P[B]≠0 ¿Pueden ser independientes?
-
César
el 4/11/17Adrián
el 4/11/17 -
Hola,soy de 4°de la eso,les agradecería mucho que me explicaran como representar intervalos geométricamente, muchas gracias
Ángel
el 4/11/17 -
Antonio Silvio Palmitano
el 4/11/17Observa que el dominio de la función es: D = (0,4].
Observa que es una función definida en dos trozos, y que las expresiones de los trozos corresponden a funciones continuas. Luego, observa que el punto de corte entre trozos es x = 2, por lo que debes estudiar para él la continuidad de la función por medio de la definición:
1°)
f(2) = 12 - 22 = 12 - 4 = 8;
2°)
Límites laterales:
Lím(x→2-) f(x) = Lím(x→2-) (12 - x2) = 12 - 22 = 12 - 4 = 8,
Lím(x→2+) f(x) = Lím(x→2+) ( (x- 4)2 + 4 ) = (2 - 4)2 + 4 = (-2)2 + 4 = 4 + 4 = 8,
y como los límites laterales son iguales, tienes:
Lím(x→2) f(x) = 8;3°)
f(2) = Lím(x→2) f(x) = 8, por lo tanto la función es continua en el punto de corte (x = 2),
y, por lo tanto, es continua en todo su dominio.
Luego, plantea la expresión de la función derivada para cada trozo:
f ' (x) =-2x si 0 < x < 2 (observa que esta expresión se anula para x = 0, que no pertenece al dominio de la función)
-4 si x = 2 (observa que los límites laterales de la función derivad coinciden para x = 2).
2(x - 4) si 2 < x < 4 (observa que esta expresión se anula para x = 4, que es extremo derecho del intervalo dominio de la función).
Luego, evalúa el límite para x tendiendo a 0 por la derecha de la función:
Lím(x→0+) f(x) = Lím(x→0+) (12 - x2) = 12,
por lo que tienes que el empleado tarda 12 horas aproximadamente en realizar la tarea cuando no tiene experiencia.
Luego, evalúa:
f(2) = 8,
por lo que tienes que el empleado tarda 8 horas en realizar la tarea cuando tiene dos meses de experiencia;
f(4) = (4 - 4)2 + 4 = 02 + 4 = 4,
por lo que tienes que el empleado tarda cuatro horas en realizar la tarea cuando tiene cuatro meses de experiencia;
luego, tienes que la función presenta un mínimo en x = 4, y el valor de la función para él es: f(4) = 4.
Espero haberte ayudado.
-
Necesito saber como hacer estos problemas:
1.- Una población sufre una fuerte emigración y en 10 años se ve reducida a la cuarta parte. Su decrecimiento es exponencial, del tipo P(t)= Po.e elevado a menos kt, donde r es la tasa de decrecimiento(en tanto por uno) y t el tiempo medido en años. Calcula k . Si la población actual es de 13,3 millones de habitantes ¿Cual será la población estimada dentro de dos años y medio?
2.- Un individuo invirtió 60000 euros repartidos en tres empresas y obtuvo 4500 euros de beneficio. Clacular la inversión realizada en cada empresa, sabiendo que en la empresa A hizo el doble de inversión que en la B y C juntas y que los beneficios de las empresas fueron del 5% en la empresa A, 10% en la B y 20% en la C.
Gracias
Antonio Silvio Palmitano
el 4/11/171)
Plantea la expresión de la función:
P(t) = P0*e-k*t;
luego, plantea para la población inicial, P(0):
P0*e-k*0 = P0*e0 = P0*1 = P0;
luego, plantea la población a los diez años, P(10):
(1/4)*P0 = P0*e-k*10, aquí haces pasaje de factor como divisor, y queda:
1/4 = e-k*10, compones en ambos miembros con la función inversa de la función exponencial natural, y queda:
ln(1/4) = -k*10, aplicas la propiedad del logaritmo del recíproco de un número en el primer miembro, y queda:
-ln(4) = -k*10, divides en ambos miembros de la ecuación por -10, y queda:
(1/10)*ln(4) = k.
Luego, tienes la población inicial (P0 = 13,3, en millones de habitantes), reemplazas en la expresión de la función, y queda:
P(t) = 13,3*e-(1/10)*ln(4)*t.
Luego, evalúa la expresión de la función para el instante en estudio (t = 2,5 = 5/2, en años):
P(5/2) = 13,3*e-(1/10*ln(4)*(5/2) = 13,3*e-(1/4)*ln(4) ≅ 9,40 millones de habitantes.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 4/11/172)
Puedes comenzar por designar: a, b, c a las sumas de dinero invertidas en las empresas A, B, C, respectivamente.
Luego tienes que la inversión total es 60000 euros, por lo que puedes plantear la ecuación:
a + b + c = 60000 (1).
Luego, tienes que la suma invertida en la empresa A es el doble de la inversión en las empresas B y C juntas, por lo que puedes plantear la ecuación:
a = 2*(b + c), aquí distribuyes y queda: a = 2b + 2c (2).
Luego, tienes el beneficio obtenido y los beneficios individuales de las empresas, por lo que puedes plantear la ecuación:
0,05a + 0,10b + 0,20c = 4500, aquí multiplicas por 20 en todos los miembros de la ecuación, y queda: a + 2b + 4c = 90000 (3).
Luego, sustituyes la expresión señalada (2) en las ecuaciones señaladas (1) (3), distribuyes, reduces términos semejantes, y queda el sistema:
3b + 3c = 60000, aquí divides por 3 en todos los términos de la ecuación, y queda: b + c = 20000, haces pasaje de término, y queda: c = 20000 - b (4),
4b + 6c = 90000, aquí divides por 2 en todos los términos de la ecuación, y queda: 2b + 3c = 45000 (5).
Luego, sustituyes la expresión señalada (4) en la ecuación señalada (5), y queda:
2b + 3(20000 - b) = 45000, distribuyes, haces pasaje de término, reduces términos semejantes, y queda:
-b = -15000, multiplicas en ambos miembros de la ecuación por -1, y queda: b = 15000 euros;
luego, reemplazas el valor remarcado en la ecuación señalada (4), y queda: c = 5000 euros;
luego, reemplazas los valores remarcados en la ecuación señalada (2), y queda: a = 40000 euros.
Espero haberte ayudado.
-
Antonius Benedictus
el 4/11/17Usuario eliminado
el 4/11/17Además he encontrado esta teoría donde me aparecen 8 casos de límite, pero aun no me han quedado clara sus diferencias, por favor me podrías explicar eso?
http://matematica.50webs.com/limite-infinito.html
Muchas gracias
-
Necesito saber como puedo resolver el siguiente sitema de dos ecuaciones:
901 = [ 337.82 / (1 + (x/365*150)) ] + [ 844.55 / (1 + (y/365*150)) ]
901 = [ 337.82 / (1 + (y/365*150)) ] + [ 844.55 / (1 + (x/365*150)) ]
Gracias
Antonio Silvio Palmitano
el 4/11/17Vamos con una orientación.
Puedes plantear las sustituciones (cambios de variable):
u = 1/( 1 + x/(365*150) ) (1),
v = 1/( 1 + y/(365*150) ) (2),
luego sustituyes, y el sistema queda:
901 = 337,82*u + 844.55*v
901 = 337,82*v + 844,55*u,
y observa que tienes para resolver un sistema de dos ecuaciones lineales, de primer grado y con dos incógnitas,
luego lo resuelves, y para terminar, tendrás que reemplazar valores en las expresiones señaladas (1) (2).
Espero haberte ayudado.