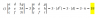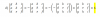-
Hola Unicoos, qué significa que un limite que tiende a +infinito me de como resultado + infinito?
Ángel
el 3/11/17En el contexto al que te refieres (el ejercicio de ayer):
" Buscamos un caso en el que podamos contradecir la universalidad implícita del enunciado:
(lim(x->inf) (f(x)-g(x)) existen) → (lim(x->inf) f(x) y lim(x->inf) g(x) no existen)
f(x) = x + 1
g(x) = x
f(x) - g(x) = x + 1 - x = 1
lim(x->inf) f(x) = infinito-------> significa que no existe límite
lim(x->inf) g(x) = infinito---------> significa que no existe límite
Entonces se cumple que:
(lim(x->inf) (f(x)-g(x)) existen) → (lim(x->inf) f(x) y lim(x->inf) g(x) no existen)
y podemos concluir que la proposición es falsa. "
-
Buenas,
Necesito averiguar el dominio de la siguiente función:
Ln (X2 - 4X - 5)
Las raices son X=5 y X=-1
Ahora debo observar el resultado de la funcion en los intervalos:
-infinito, -1
-1,5
5, +infinito
Los valor negativos y 0 no son posibles en el Ln.
Si tomo el valor X=-2 el resultado es Y=Ln -9, lo cual no es posible.
Para X=-1el resultado es Ln 0, lo cual no es posible.
Por lo tanto de -infinito a -1 la función no existe?
Mi duda es que si tomo X=-100 por ej el resultado es un número positivo Y=9,24
Entonces para valores muy grandes y negativos vale la función?
Para X=0 Y=Ln -5 No es posible la función
Para X=5 Y=Ln 0 No es posible la función
Para X=6 Y=Ln 7 Es posible la función en el intervalo (5, +infinito)
Gracias!
Saludos
-
Perdón en el sistema que envié justo antes me confundí y donde está la "a" es un 1: el sistema queda así:
2z+y+(b+1)x=1
b*y+(b+1)x=1
(2b+2)x=b+2
-
Buenos días
Tengo una duda de como despejar dos incógnitas en éste sistema equivalente que me resulta después de aplicar Gauss:
2*z+y+(b+a)x=1
b*y+(b+a)x=1
(2b+2)x=b+2
Despejar x si lo ví claro: x= b+2/(2b+2)
cómo sería para despejar z e y?por favor?
gracias de antemano
Saludos cordiales,
Irene
-
en relación a mi ultima pregunta https://www.unicoos.com/discusion/160743# mi profesora dice que no es correcta mi respuesta (ella asegura que son 16), yo se que esta bien razonado 32, coincido con angel .
¿Qué puedo hacer?
Antonius Benedictus
el 3/11/17Antonio Silvio Palmitano
el 3/11/17Observa que si las bacterias se reproducen cada 45 minutos tendría razón tu Profesora.
Por las dudas haya error en tu enunciado, por favor corrobora que esté correcto, y si lo está, coincido con el colega Antonio en que debes pedir justificación formal, porque los docentes también nos equivocamos de vez en cuando.
Espero haberte ayudado.
Ángel
el 3/11/17Como te dicen los profes, tendrás que contrastar con tu libro y/o tutor.
Además aprovecho para decir que considero que estos enunciados son de naturaleza ambigua, ya que no nos informa de la "edad" de la bacteria a la hora de empezar a contar y con las matemáticas podemos inferir ciertas cosas...¡pero no adivinarlas que yo sepa!
(aunque tendemos a interpretarlo como en el caso 1 o caso 3 por facilidad a la hora de modelizarlo con una fórmula)
Si no tenemos claro si son 35 o 45 minutos, puedes decir que a las 3 horas hay 16,32 o 64; y si lo justificas con palabras sería correcto:
Caso 1: Si la bacteria nació justo antes de empezar a contar los minutos y se reproduce cada 35 min
Minuto 0 ---> 1 bacteria
Minuto 35 ---> 2 bacterias
Minuto 70 ---> 4 bacterias
Minuto 105 ----> 8 bacterias
Minuto 140 ----> 16 bacterias
Minuto 175 -----> 32 bacterias a las 3 horas
Caso 2: Si la bacteria nació 34 min y 59seg antes de empezar a contar los minutos y se reproduce cada 35 min
Minuto 0 ---> 2 bacterias
Minuto 35 ---> 4 bacterias
Minuto 70 ---> 8 bacterias
Minuto 105 ----> 16 bacterias
Minuto 140 ----> 32 bacterias
Minuto 175 -----> 64 bacterias a las 3 horas
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Caso 3: Si la bacteria nació justo antes de empezar a contar los minutos y se reproduce cada 45 min
Minuto 0 ---> 1 bacteria
Minuto 45 ---> 2 bacterias
Minuto 90 ---> 4 bacterias
Minuto 135 ----> 8 bacterias
Minuto 180 ----> 16 bacterias a las 3 horas
Caso 4: Si la bacteria nació 44 min y 59seg antes de empezar a contar los minutos y se reproduce cada 45 min
Minuto 0 ---> 2 bacterias
Minuto 45 ---> 4 bacterias
Minuto 90 ---> 8 bacterias
Minuto 135 ----> 16 bacterias
Minuto 180 ----> 32 bacterias a las 3 horas
-
Necesito resolver la siguiente ecuación exponencial: 921,95 = (7000 * e 0.48 *x) - ( 12000 * e 0.48 * (x+15))
donde x es la incógnita
Antonio Silvio Palmitano
el 3/11/17Por favor, verifica que hayas consignado correctamente la ecuación.
De todas maneras, vamos con tu ejercicio.
Distribuyes en el exponente del segundo factor en el último término, y queda:
921,95 = 7000*e0,48*x - 12000*e0,48*x+7,2.
Aplicas la propiedad del producto de potencias con bases iguales en el segundo factor en el último término, y queda:
921,95 = 7000*e0,48*x - 12000*e0,48*e7.2.
Extraes factores comunes en el segundo miembro, y queda:
921,95 = 1000*e0,48*x*(7 - 12*e7.2).
Haces pasajes de factores como divisores, y queda:
921,95 / ( 1000*(7 - 12*e7.2) ) = e0,48*x.
Resuelves el primer miembro, y queda:
-5,738*10-5 ≅ e0,48*x,
y observa que es una ecuación que no tiene solución, porque el primer miembro es negativo, y la expresión del segundo miembro toma valores estrictamente positivos.
Espero haberte ayudado.
-
Hola! Tengo una duda con este integral, tengo que resolverlo aplicando el método de INTEGRACIÓN POR PARTES, pero no sé si tengo que aplicar el método de sustitución antes o si es posible usar dos métodos en una sola integral, estoy confundida. Este es el ejercicio: ∫x√x+2dx (ACLARACIÓN: "x+2" está dentro de la raíz cuadrada, por si no se entiende bien).
Sofía Martinez
el 3/11/17Antonio Silvio Palmitano
el 3/11/17Puedes plantear:
u = x, de donde tienes: du = dx,
dv = √(x+2)dx = (x+2)1/2dx, de donde tienes: v = (2/3)(x+2)3/2;
luego aplicas el método y la integral queda:
I = uv - ∫ vdu = (2/3)x(x+2)3/2 - (2/3) ∫ (x+2)3/2dx;
luego resuelves la integral secundaria, y queda:
I = (2/3)x(x+2)3/2 - (4/15)x(x+2)5/2 + C.
Espero haberte ayudado.
-