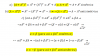-
Buenas,una pequeña consulta, para el apartado a,¿ la distancia es desde el punto (0,0) o cuando el tiempo es igual a 0 (t=0)?
Gracias
XenoPhenom
el 1/11/17Esto es de física, no de matemáticas. Pero de todas formas lo único que tienes que hacer es sustituir la t por 5 y ya tendrás el vector r en ese instante. En el apartado b simplemente derivas en función del tiempo y luego sustituyes t por 5 y listo. Es un ejercicio sin más complicación.
Antonio Silvio Palmitano
el 1/11/17a)
Evalúa la posición para el instante en estudio, y luego plantea su desplazamiento con respecto al origen ( r0 = < 0,0 >),
y luego evalúas el módulo de dicho desplazamiento, y tienes para la distancia al origen a los cinco segundos:
d = |r(5) - r0| = |r(5) - <0,0>| = cancelas el término nulo = |r(5)|.
Observa que el instante inicial es t = 0, pero observa también que en dicho instante el móvil no se encuentra en el origen de coordenadas, porque su posición inicial es: r(0) = < 24,4 ; 74,4 > (en metros).
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 1/11/17Si el grado es 1, tienes que los coeficientes de los términos de grado tres y de grado dos son iguales a cero, por lo que puedes plantear:
2a + b = 0, haces pasaje de término, y queda: b = - 2a (1)
a2 + b + 1 = 0,
luego, sustituyes la expresión señalada (1) en la segunda ecuación, y queda:
a2 - 2a + 1 = 0,
que es una ecuación polinómica cuadrática con una solución real: a = 1,
luego, reemplazas en la ecuación señalada (1) y queda: b = -2.
Luego, reemplazas los valores remarcados en la inecuación del enunciado, cancelas los términos nulos (que son los términos con grado tres y grado dos), y queda:
x + 1 ≥ 0,
haces pasaje de término, y queda:
x ≥ -1.
Por lo tanto, tienes que la opción (A) es la respuesta correcta.
Espero haberte ayudado.
-
Entiendo lo que quiere decir el ejercicio y lo puedo probar con matrices concretas que me invento, pero no sé demostrarlo para cualquier matriz de orden n.
XenoPhenom
el 1/11/17Antonius Benedictus
el 2/11/17 -
 Buenos días, me dirían si esta bien resuelto? Gracias. Una caja contiene 5 bolas blancas y 4 negras, otra caja contiene 3 bolas blancas y 6 negras. Se pasa una bolillo de la primera caja a la segunda y luego de esta segunda se extrae una bolilla que se pasa a la primera caja. ¿Cu al es la probabilidad de que al extraer una bolilla de la primera sea blanca?
Buenos días, me dirían si esta bien resuelto? Gracias. Una caja contiene 5 bolas blancas y 4 negras, otra caja contiene 3 bolas blancas y 6 negras. Se pasa una bolillo de la primera caja a la segunda y luego de esta segunda se extrae una bolilla que se pasa a la primera caja. ¿Cu al es la probabilidad de que al extraer una bolilla de la primera sea blanca? -
Me podrían ayudar con este ejercicio:
las bacterias se reproducen de forma asexual y muy rápidamente. Supón que una bacteria se reproduce cada 35 minutos. Calcula cuantas se habrán formado al cabo de 3 horas. Representa el crecimiento.
Ángel
el 1/11/17Intuitivamente:
Minuto 0 ---> 1 bacteria
Minuto 35 ---> 2 bacterias
Minuto 70 ---> 4 bacterias
Minuto 105 ----> 8 bacterias
Minuto 140 ----> 16 bacterias
Minuto 175 -----> 32 bacterias
A las tres horas hay 32 bacterias (porque la próxima "reproducción" será a las 3 horas y media, ya pasado el intervalo de estudio)
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Formalmente:
La curva (exponencial) que representa el crecimiento de la población de bacterias es C(x)=2(x/35)-(parte decimal de x/35) ,
donde x es el tiempo de estudio y C(x) la función crecimiento.
Aplicado a nuestro ejemplo:
3 horas= 180 minutos
180÷35= 5,14...
Restamos la parte decimal y obtenemos el exponente:
5,14.... - 0.14.... = 5
C(180)=25= 32 bacterias a los 180 minutos (3 horas)
**En cursos posteriores verás esta función https://www.ditutor.com/funciones/parte_entera.html
y podrías expresar la función crecimiento como C(x)=2E(x/35)
-
Alguien me puede explicar por que no me da bien?? Se supone que la solucion es (1,2,3) . Hemos de hacerlo por este metodo de Gauss( que es por reduccion) que alguien me ayudee
Antonio Silvio Palmitano
el 1/11/171°)
Mantienes la primera ecuación, a la segunda ecuación le restas el doble de la primera, a la tercera ecuación le restas la primera ecuación multiplicada por 6, y queda el sistema:
x + 3y + 4z = 19
-11y - 7z = -43
-21y -25z = -117.
2°)
Mantienes la primera ecuación, a la segunda la multiplicas por -21 y a la tercera la multiplicas por -11, y queda:
x + 3y + 4z = 19
231y + 147z = 903
231y + 275z = 1287.
3°)
Mantienes la primera ecuación, a la tercera ecuación le restas la segunda, divides por 21 en todos los términos de la segunda ecuación, y queda:
x + 3y + 4z = 19
11y + 7z = 43
128z = 384,
haces pasaje de factor como divisor en la tercera ecuación, y queda: z = 3.
4°)
Reemplazas el valor remarcado en las dos primeras ecuaciones, haces pasajes de términos, y queda:
x + 3y = 7
11y = 22,
haces pasaje de factor como divisor en la segunda ecuación, y queda: y = 2.
5°)
Reemplazas en la primera ecuación, haces pasaje de término, y queda: x = 1.
Luego, tienes que el conjunto solución queda:
S = { (1,2,3) }.
Espero haberte ayudado.