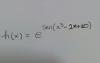-
Antonio Silvio Palmitano
el 31/10/17Tienes la expresión de la función: y =f(x) = epx,
luego, plantea la expresión de su función derivada: y ' = f ' (x) = p*epx.
Luego, plantea las coordenadas del punto de contacto (observa que tienes en el enunciado que su abscisa es igual a 1): A(1,ep*1),
resuelves la ordenada, y queda: A(1,ep)
Luego, plantea la pendiente de la recta tangente: m = f ' (1) = p*ep*1 = p*ep.
Luego, con las coordenadas del punto de contacto, y con la expresión de la pendiente, plantea la ecuación de la recta tangente:
y - ep = p*ep*(x - 1);
luego, como tienes en el enunciado que el punto O(0,0) pertenece a la recta tangente, reemplazas sus coordenadas, y queda:
0 - ep = p*ep*(0 - 1),
cancelas términos nulos, resuelves en el segundo miembro, y queda:
- ep = - p*ep,
divides en ambos miembros por - ep (observa que es una expresión que toma valores estrictamente menores que cero), y queda:
1 = p.
Espero haberte ayudado.
-
 Hola Unicoos!! Espero que me podáis ayudar en este ejercicio. Es sobre la discusión de sistemas y además resolverlo. Lo que me pasa es que la solución me pone que es un "S.C.I" y a mí me sale un "S.I". Por lo cual yo ya no resolvería. Espero que ne digáis en qué he fallado o si se hace de otra forma. gracias
Hola Unicoos!! Espero que me podáis ayudar en este ejercicio. Es sobre la discusión de sistemas y además resolverlo. Lo que me pasa es que la solución me pone que es un "S.C.I" y a mí me sale un "S.I". Por lo cual yo ya no resolvería. Espero que ne digáis en qué he fallado o si se hace de otra forma. graciasAntonio Silvio Palmitano
el 31/10/17Plantea la matriz ampliada del sistema:
1 1 0 -1 1
0 1 2 2 2
-1 0 2 3 1
A la tercera fila le sumas la primera fila, y queda:
1 1 0 -1 1
0 1 2 2 2
0 1 2 2 2
A la tercera fila le restas la segunda fila, y queda:
1 1 0 -1 1
0 1 2 2 2
0 0 0 0 0.
Observa que la matriz ampliada escalonada y equivalente por filas tiene dos filas no nulas,
por lo que tienes que el rango de la matriz del sistema es igual al rango de la matriz ampliada, que es igual a dos,
y como el sistema tiene cuatro incógnitas, puedes concluir que el sistema es compatible indeterminado y admite
infinitas soluciones, según el Teorema de Rouché-Frobenius.
Espero haberte ayudado.
-
Hola Unicoos, me echan una mano, no sé cómo hacerlo.
Dada la función h(x), calcula el valor de su derivada en x=0, sabiendo que f(0)=0 y f'(0)=1 .
Muchas gracias
Antonio Silvio Palmitano
el 31/10/17¿Puede ser que te haya faltado parte del enunciado en la foto? Observa que tienes solamente la expresión de la función h, pero no tienes información alguna sobre la función f.
De todas maneras, para obtener la expresión de la función derivada de h, aplicas la regla de la cadena, y queda:
h ' (x) = esen(x^3-2x+10)*cos(x3-2x+10)*(3x2-2).
Espero haberte ayudado.
-
Hola Unicoos.
He hecho bien el ejercicio?
En el último apartado, no puedo calcular la recta tangente verdad? Porque no me dan ningún punto.
Muchas gracias.
David
el 15/11/17No te piden la recta tangente, solo los puntos en los que la tangente es horizontal.
El cosx=0 para x=PI/2 y para x=3PI/2 ...
Y sí podrías hacer la recta tangente, para esos valores de x.... Sería y-sen(PI/2)= 0.(x-PI/2)... y-1=0... y=1.
Lo mismo para 3PI/2, que te quedaría y=-1... Pero no te lo piden.
BESOS!! -
Antonius Benedictus
el 30/10/17Voy a interpretar U_A como el vector A normalizado (esto es, misma dirección y sentido que A y módulo 1 o unitario)
a) La suma de dos vectores unitarios no es otro vector unitario(en general).
b) El vector C es la diagonal de un paralelogramo. En cambio, el C es la diagonal de un rombo o un cuadrado encajado en el paralelogramo. Salvo que A y B midan lo mismo, C y D no tienen la misma dirección.
c) Sin sentido.
d) La respuesta.