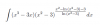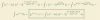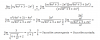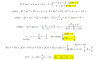-
Una empresa de azucar esta considerando cambiar el empaquetado de bolsas de azucar a cajas. El incremento del coste sería de 0.5p cada una, lo cual reduciría el beneficio de 5.5p a 5.0p. La caja sería más conveniente para los clientes y podría generar ventas extras. Se considera la probabillidad de un 20% de aumento en las ventas a el 0.6 (la alternativa es que no cambie). El horizonte son dos años, durante los que se espera vender 1 millon de paquetes. Dibuja un arbol de decisión para evaluar el cambio de empaquetamiento con los respectivos EMV (en ingles).
Antonius Benedictus
el 28/9/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Hola chicos,
Soy un poco atascado en probabilidades y estadistica y me gustaria a ver si me pudiérais echar una mano con unos ejercicios con los que me he cruzado.
Muchas gracias de antemano. Seguir así.
1- Dos empresas M y H están en peligro de quiebra, analistas consideran que para el año que viene P(M quiebre)= 0.7, P(H quiebre)= 0.6 y P(M y H quiebren)= 0.5
-¿Cual es la probabilidad de que M quiebre y H sobreviva?
- ¿Cual es la probabilidad de que las dos sobrevivan?
-
Hola, me podría ayudar a hacer este ejercicio ??
Por favor no me lo marquen como "spam". Me gustaría que me ayudara a resolverlo ( Lo vuelvo a colocar porque no me a respondido y veo que a los otro sí, a lo cual asumí que se le pasó la pregunta). Por su atencion muchas gracias.
Jesus Garcia
el 28/9/17 -
Antonius Benedictus
el 27/9/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Pedro..WrF
el 27/9/17 -
a) El conjunto de positividad me dio el intervalo (4;7)
B) me dio qe n tiene asintota h, av es igual a x=2 y asint oblicua y=5x-10
D) an convrrge a 0 por lo tanto esta acotada pero seguro esta mal este
-
Antonio Silvio Palmitano
el 27/9/173)
Observa que para x = 3, la ordenada en la recta tangente es: y = 2*3-1 = 5, por lo que el punto de contacto es A(3,5).
Luego, observa que la pendiente de la recta tangente es m = 2
Luego, con la ordenada del punto de contacto tienes: f(3) = 5, y con la pendiente de la recta tangente tienes: f ' (3) = 2.
Luego, tienes la ecuación que define implícitamente a la función g, derivas y queda:
y ' * ln(x-2) + 1*y2 + x*2*y*y ' = 0,
reemplazas las coordendas del punto en estudio: (3,2), y queda:
y ' * ln(3-2) + 1*(2)2 + (3)*2*(2)*y ' = 0,
resuelves coeficientes en los términos, y queda:
y ' * 0 + 4 + 12*y ' = 0,
cancelas el término nulo, haces pasaje de término, y queda:
12*y ' = - 4,
haces pasaje de factor como divisor, y queda:
y ' = - 1/3;
luego, con la ordenada del punto en estudio tienes: g(3) = 2, y con el valor de la derivada tienes: g ' (3) = - 1/3.
Luego, tienes la función producto:
h(x) = f(x)*g(x),
luego, plantea la expresión de su función derivada (observa que debes aplicar la regla del producto):
h ' (x) = f ' (x) * g(x) + f(x) * g ' (x),
luego, evalúa la expresión para x = 3:
h ' (3) = f ' (3) * g(3) + f(3) * g ' (3),
reemplazas los valores remarcados, y queda:
h ' (3) = 2*2 + 5*(-1/3) = 4 - 5/3 = 7/3.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 27/9/174)
Plantea la expresión de la función derivada (observa que debes aplicar la regla del producto, y la regla de la cadena en el segundo factor):
f ' (x) = 3*(x - 2)2*ek/(x-2) + (x - 2)3*ek/(x-2)*( -k/(x-2)2 ).
Luego, como la función presenta un punto crítico en x = 4, plantea:
f ' (4) = 0,
evalúas la función derivada para x = 4, sustituyes en el primer miembro, y queda:
3*(4 - 2)2*ek/(4-2) + (4 - 2)3*ek/(4-2)*( -k/(4-2)2 ) = 0,
resuelves coeficientes y exponentes, y queda
12*ek/2 + 8*ek/2*(-k/4) = 0,
resuelves signos y coeficiente en el segundo término:
12*ek/2 - 2*k*ek/2 = 0,
extraes factores comunes, y queda:
2*ek/2*(6 - k) = 0,
haces pasajes de factores como divisores (observa que el factor exponencial es estrictamente mayor que cero), y queda
6 - k = 0,
haces pasaje de término y queda:
6 = k.
Luego, la expresión de la función queda:
f(x) = (x - 2)3*e6/(x-2),
luego, evalúa para los extremos del intervalo, y para el punto crítico que pertenece a él:
f(3) = (3 - 2)3*e6/(3-2) = 1*e6 = e6 ≅ 403,4288;
f(4) = (4 - 2)3*e6/(4-2) = 8*e3 ≅ 160,6843;
f(5) = (5 - 2)3*e6/(5-2) = 27*e2 ≅ 199,5045.
Luego, puedes concluir que la función presenta, para el intervalo cerrado [3,5]:
Máximo Absoluto en x = 3, y el valor de la función para él es: f(3) = e6;
Mínimo Absoluto en x = 4, y el valor de la función para él es: f(4) = 8*e3.
Espero haberte ayudado.
-
podrían explicarme esta demostración DEMOSTRAR: No existe z ∈ R Tal que x=<z para todo x ∈ R
Antonio Silvio Palmitano
el 27/9/17Lo puedes demostrar por Reducción al Absurdo.
Supuesto Absurdo: existe z ∈ R tal que, para todo x ∈ R se cumple que x ≤ z (1).
Probaremos que existe z ∈ R tal que para todo x ∈ R se cumple que x ≤ z, y z < x, lo cuál es contradictorio.
Luego, para demostrar, plantea:
si z ∈ R, entonces x = z + h ∈ R (ley de cierre de la suma en R), con h ∈ R, h > 0, luego tienes: x ∈ R,
luego, observa que tienes:
z < z + h, por lo tanto: z < x,
lo cuál contradice al supuesto absurdo.
Espero haberte ayudado.
-
ayudame con este por favor.
Cuando en baloncesto un jugador encesta una canasta, ésta puede tener el valor de 1 punto, 2 puntos ó 3 puntos, dependiendo de ciertas condiciones del lanzamiento. En la pasada jornada el equipo Local consiguió un total de 85 puntos en los 39 tiros encestados.
Determine cuántas canastas de cada tipo encestó sabiendo además que el número de triples fue doble que el numero de canastas de 1 punto.
Jordi García
el 27/9/17x → lanzamientos de 1 punto
y → lanzamientos de 2 puntos
z → lanzamientos de 3 puntos
Sistema de 3 incógnitas:
x + y + z = 39
x + 2y + 3z = 85
z = 2x
Si lo resuelves te tiene que salir la siguiente solución:
{x = 7, y = 18, z = 14}
Resolver sistema de 3 ecuaciones con 3 incógnitas
https://www.youtube.com/watch?v=klWAnkzOIbo
https://www.vitutor.com/ecuaciones/2/gauss.html
O puedes sustituir el z = 2x en ambas ecuaciones y plantear un sistema de 2 ecuaciones.
Espero que lo entiendas.
Jordi García
el 29/9/17Por supuesto, aquí lo tienes:
1. Sustituimos z = 2x en ambas ecuaciones:
x + y + z = 39 → x + y + 2x = 39 → 3x + y = 39
x + 2y + 3z = 85 → x + 2y + 3(2x) = 85 → 7x + 2y = 85
2. Utilizamos el método de sustitución para resolver el sistema:
2.1 Despejamos una incógnita en una de las ecuaciones:
3x + y = 39 → y = 39 - 3x
2.2 Sustituimos en la otra ecuación y resolvemos:
7x + 2y = 85 → 7x + 2(39 - 3x) = 85 → 7x + 78 - 6x = 85 → x + 78 = 85 → x = 85 - 78 → x = 7
2.3 Hallamos la otra incógnita
y = 39 - 3x → y = 39 - 3 · 7 = 39 - 21 → y = 18
3. Como hemos sustituido al principio z = 2x, sabiendo x podemos calcular z:
z = 2x → z = 2 · 7 → z = 14
Solución: {x = 7, y = 18, z = 14}
Saludos!