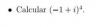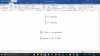
Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

necronomicion00
el 27/9/17

••0 voto/s
•
Antonius Benedictus
el 27/9/17
Inecuaciones con valores absolutos
•0 voto/s
•
Desencadenado
el 27/9/17

•0 voto/s
•

Cancelar
necronomicion00
el 27/9/17

Antes formulé mal el enunciado.

••0 voto/s
•
Antonius Benedictus
el 27/9/17
Números complejos
•0 voto/s
•
Desencadenado
el 27/9/17

•0 voto/s
•

Cancelar
MARC CORDERO JORDANA
el 27/9/17

buenas;
utilizandon la fórmula trigonometrica de ( sen(2x), cos(2x), sen(3x), o cos(3x) ) Utilizando la que haga falta *

Demuestre:

cos (π/6) = √3/2
sen(π/8) =

••0 voto/s
•
Antonius Benedictus
el 27/9/17

•0 voto/s
•

Cancelar
necronomicion00
el 27/9/17

Resolver cos2 x = cos x

••0 voto/s
•
MARC CORDERO JORDANA
el 27/9/17
buenas;
cos(2x) no es igual a cosx
si te sale en un ejercicio o algo pasa la foto para poder verlo mejor porfa ;)

•0 voto/s
•
Ángel
el 27/9/17
cos²x-sen²x=cosx
cos²x-cosx= sen²x
cos²x-cosx= 1-cos²x
2cos²x-cosx-1=0
Cambio: t=cosx
2t²-t-1=0
t=1 -----> cosx= 1 -------> x= 0º+360K
t= -1/2 -----> cosx= -1/2 -----> x= 120º+360K     ,     x=240+360K

Las 3 soluciones podrían englobarse en una: x= 0º+120K

•0 voto/s
•
necronomicion00
el 27/9/17
vale ahora lo subo correctamente con imagen

•0 voto/s
•
Ángel
el 27/9/17
Marc, cos(2x)=cosx es una ecuación trigonométrica que para los valores 0º+120K sí es igual.

•0 voto/s
•
Antonio Silvio Palmitano
el 27/9/17
Vamos con algunas precisiones.
1)
Si tienes la identidad:
cos(2x) = cosx,
aplicas la identidad del coseno del doble de un ángulo en el primer miembro, y queda:
cos²x - sen²x = cosx,
aplicas la identidad del cuadrado del seno en función del cuadrado del coseno en el segundo término, y queda:
cos²x - (1 - cos²x) = cosx ,
distribuyes el agrupamiento, reduces términos semejantes, y queda:
2*cos²x - 1 = cosx,
haces pasaje de término, ordenas términos, y queda:
2*cos²x - cosx - 1 = 0,
aplicas la sustitución (cambio de incógnita): w = cosx (1), y queda:
2*w² - w - 1 = 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son:
a)
w = 1, sustituyes la expresión señalada (1) y queda:
cosx = 1, compones en ambos miembros con la función inversa del coseno, y queda:
x = 2*k*π, con k ∈ Z;
b)
w = -1/2,
sustituyes la expresión señalada (1) y queda:
cosx = -1/2, compones en ambos miembros con la función inversa del coseno, y quedan dos opciones:
b₁)
x = 2π/3 + 2*m*π, con m ∈ Z (en el segundo cuadrante),
b₂)
x = -2π/3 + 2*n*π, con n ∈ Z (en el tercer cuadrante).
Observa que hemos expresado las soluciones en radianes (recuerda: 180° = 1 radián).
Espero haberte ayudado.

•0 voto/s
•
necronomicion00
el 27/9/17
Este es el enunciado correcto

•0 voto/s
•
Ángel
el 27/9/17
cos2x=cosx -------> cos2x-cosx=0 ------
------> cosx(cosx-1)=0 ----->      cosx= 0  ,       cosx=1
----------> arccos(0)= x= 90º+360K ,   arccos(1)= x= 0º+360K

•0 voto/s
•

Cancelar
necronomicion00
el 27/9/17

Calcular (−1 + i) 4

••0 voto/s
•
MARC CORDERO JORDANA
el 27/9/17
aplicando la propiedad distributiva de la multiplicación;
(-1)·4 + i·4 = -4 +4i

•0 voto/s
•
necronomicion00
el 27/9/17
esta mal el enunciado ahora los subo de nuevo con imagen pero gracias

•0 voto/s
•

Cancelar
David Ru
el 27/9/17

Hola , estoy intentando resolver esta ecuación contextualizada utilizando máximos y mínimos ( con la ayuda de derivadas ) y no consigo resolverlo , podíais desarrollarlo , para ver como resolver este tipo de ejercicios y en que me estoy equivocando ? , la solucion es lado rectangulo 100 , diametro semicirculo 200/ pi , gracias
Un campo de atletismo de 400 metros de perímetro , consta de un rectangulo y dos semicirculos en sus extremos , halle las dimensiones para que el área del retángulo sea la mayor posible .

••0 voto/s
•
Antonius Benedictus
el 27/9/17

•1 voto/s
•

Cancelar
Mk3
el 27/9/17

Hola,
A ver si alguien me puede echar un cable y decirme que hago mal, la solución que da el libro es: (100√2≈141km/h).
Adjunto enunciado del problema y mi desarrollo.
Gracias anticipadas!!

••0 voto/s
•
Antonius Benedictus
el 27/9/17

•1 voto/s
•

Cancelar
Ángel
el 27/9/17

Determinar la forma clausulada:
{ ( ¬p→ ¬q) ∨ [(r→p)∧(s→q)] } → ( ¬r v ¬s)

Comprobar construyendo su fórmula clausulada si estas dos proposiciones son equivalentes:
(¬p v ¬q) ∧ (r→p) ∧ (s→q) y ¬(r ∧ s)

••0 voto/s
•
David
el 11/10/17
Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

•0 voto/s
•
Ángel
el 30/11/17
:)

•0 voto/s
•

Cancelar
Paula
el 27/9/17

hola, podrían ayudarme con estas integrales por favor?? Gracias de ante mano, un saludo.

••0 voto/s
•
César
el 27/9/17
Integrales

Integrales

•1 voto/s
•

Cancelar