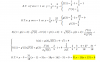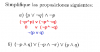1)

Separas en términos, y tienes la suma de integrales:

∫ (2*x⁴ + x²)*dx = separas en términos = ∫ 2*x⁴*dx + ∫ x²*dx = extraes el factor numérico en el primer término = 2*∫ x⁴*dx + ∫ x²*dx = integras:

= [ 2*x⁵/5 + x³/3 ] = evalúas con Regla de Barrow:

= (1⁵/5 + 1³/3) - (0⁵/5 + 0³/3) = (1/5 + 1/3) - (0 + 0) = 8/15 - 0 = 8/15.

2)

∫ x*cos(x/2)*dx =

plantea la sustitución (cambio de variable): x/2 = w (1), de donde tienes: x = 2*w, y también tienes: dx = 2*dw, sustituyes y queda:

= ∫ 2*w*cosw*2*dw = extraes factores constantes y queda:

= 4*∫ w*cosw*dw = 

aplicas el Método de integración por partes:

u = w, de donde tienes: du = dw, dv = cosw*dw, de donde tienes: v = senw:

= 4*( w*senw - ∫ senw*dw ) = integras en el segundo término del agrupamiento:

= 4*( w*senw - (- cosw) ) + C = resuelves el signo en el segundo término del agrupamiento, distribuyes en el primer término, y queda:

= 4*w*senw + 4*cosw + C =

sustituyes la expresión señalada (1) y queda:

= 4*(x/2)*sen(x/2) + 4*cos(x/2) + C =

simplificas en el primer término, y queda:

= 2*x*sen(x/2) + 4*cos(x/2) + C.

3)

∫ ( sen(√(x))/√(x) ) )*dx = 

plantea la sustitución (cambio de variable): w =√(x) (1), de donde tienes: dw = ( 1/(2*√(x)) ) *dx, y también tienes: 2*dw = ( 1/√(x) )*dx, sustituyes y queda:

= ∫ senw*2*dw = extraes el factor constante y queda:

= 2*∫ senw*dw = integras y queda:

= 2*(- cosw) + C = resuelves el primer término, y queda:

= - 2*cosw + C = sustituyes la expresión señalada (1) y queda:

= - 2*cos( √(x) ) + C.

Espero haberte ayudado.

Trigonometría - Resolución de un triángulo rectángulo

Observa que en el triángulo rectángulo tienes que los ángulos interiores A y C son complementarios, por lo tanto tienes las identidades:

cosA = senC (1), senA = cosC (2), tanA = cotgC (3), cotgA = tanC (4), secA = cosecC (5) y cosecA = secC (6).

Luego, tienes la expresión:

L = cos²A + cos²C + cotg²C, 

aplicas la identidad señalada (1) en e primer término, y queda:

L = sen²C + cos²C + cotg²C, 

aplicas la identidad fundamental (o pitagórica) para los términos remarcados, y queda:

L = 1 + cotg²C, 

aplicas la identidad de la cotangente en función del coseno y del seno, y queda:

L = 1 + cos²C/sen²C,

extraes denominador común, y queda:

L = (sen²C + cos²C)/sen²C,

aplicas la identidad fundamental (o pitagórica) en el numerador, y queda:

L = 1/sen²C,

aplicas la identidad de la cosecante en función del seno, y queda:

L = cosec²C, aplicas la identidad señalada (5) y queda:

L = sec²A.

Observa que las dos expresiones remarcadas son equivalentes.

Espero haberte ayudado.

Razones trigonométricas vs tangente

Razones trigonométricas vs tangente

Trigonometría - Resolución de un triángulo rectángulo

Trigonometría - Resolución de un triángulo rectángulo

http://www.cienciamatematica.com/librosdematematica.html

¡Muchas gracias, Antonio!, no lo veía...

El resultado final es q ∨ ¬(p v q) por Morgan, pero me quedó claro el proceder.