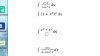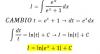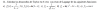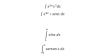-
Hola , estoy con integrales y me he quedado bloqueado en una ,sería alguien tan amble de hacerme el desarrollo ? ya que no me da lo mismo que la solución que es x^2/2 + C
Integral de e^lnx * dx
gracias
-
Antonio Silvio Palmitano
el 27/9/17Vamos con una orientación.
Son todas integrales en las que puedes aplicar el Método de Integración por Partes
1)
u = x2, de donde tienes: du = 2x*dx;
dv = e2x, de donde tienes: v = (1/2)e2x,
luego, aplicas el método y queda:
I = (1/2)x2e2x - 2*∫x*e2x*dx,
luego, observa que en la integral secundaria puedes volver a plantear el método:
u = x, de donde tienes: du = dx;
dv = e2x, de donde tienes: v = (1/2)e2x,
luego, aplicas el método y queda:
I = (1/2)x2e2x - 2*( (1/2)xe2x - (1/2)*∫e2x*dx ),
luego resuelves la última integral (observa que es directa), y queda:
I = (1/2)x2e2x - 2*( (1/2)xe2x - (1/4)e2x ) + C.
2)
u = lnx, de donde tienes: du = (1/x)*dx,
dv = x, de donde tienes: v = (1/2)x2,
luego aplicas el método, y tienes:
I = (1/2)x2lnx - (1/2)*∫ x2(1/x)*dx,
luego, simplificas en el argumento de la integral secundaria, y queda:
I = (1/2)x2lnx - (1/2)*∫ x*dx,
resuelves la integral secundaria (observa que es directa), y queda (indicamos con corchetes que debemos evaluar con Regla de Barrow entre 1 y e):
I = [ (1/2)x2lnx - (1/4)x2 ],
evalúas y queda:
I = ( (1/2)e2 - (1/4)e2 ) - ( 0 - 1/4 ) = (1/4)e2 + 1/4.
3)
u = arctanx, de donde tienes: du = ( 1/(1+x2) )*dx,
dv = x, de donde tienes: v = (1/2)x2;
aplicas el método y queda:
I = (1/2)x2arctanx - (1/2)*∫ ( x2/(1+x2) )*dx,
sumas y restas 1 en el numerador del argumento de la integral secundaria, distribuyes el denominador, simplificas, y queda:
I = (1/2)x2arctanx - (1/2)*∫ ( 1 - 1/(1+x2) )*dx,
resuelves la integral secundaria (observa que es una resta de integrales directas) y queda (indicamos con corchetes que debemos evaluar con Regla de Barrow entre 0 y 1):
I = [ (1/2)x2arctanx - (1/2)*(x - arctanx) ],
evalúas y queda:
I = ( π/8 - (1/2)*(1 - π/4) ) - ( 0 - 0) ) = π/4 - 1/2.
Espero haberte ayudado.
-
Hola, buenas tardes a tod@s.
Necesito ayuda con el Producto Cartesiano de dos conjuntos dados y su relación con la Correspondencia G de A en B (siendo G, A, B conjuntos). Agradezco, de antemano, todo tipo de ayuda (explicaciones, vídeos, ejemplos,...).
Nuevamente, daros las gracias por su respuesta.
Reciban un cordial saludo.-
Ángel
el 27/9/17Tienes que ser un poco más concreto.
Manda si quieres ejercicios que dudes y los intentamos hacer; lo que queda de semana lo dedicaré al tema de lógica de predicados-conjuntos y la semana que viene a relaciones y aplicaciones así que ya sabes.
En cuanto a los vídeos y ejemplos será mejor que especifiques la asignatura y el nivel.
Un saludo.
Usuario eliminado
el 28/9/17Soy un estudiante del primer año del Doble Grado en Matemáticas y Estadística. Mi profesor de Álgebra me ha dicho que una correspondencia G de A en B es un subconjunto del producto cartesiano de A y B, pero no llego a entender el por qué ni qué relación presenta la correspondencia con las aplicaciones. Todavía no hemos propuesto ningún ejercicio, pero si me pone uno de ejemplo, se lo agradecería muchísimo. Por cierto, ¿cómo podría seguir su tema de lógica de predicados-conjuntos?.
Muchas gracias por su atención y dedicación.
Reciba un cordial y fraternal abrazo.-
Ángel
el 29/9/17Pues puede ser que tengamos un temario parejo.
Yo he dejado aparcado el 3º del grado de Informática y este año empiezo a complementar con Grado en Matemáticas a distancia (UNED). Por lo que, aunque no tenga un conocimiento amplio de matemáticas los conceptos nuevos los conozco un poco.
El temario que seguiré hasta Enero/2018 es:
------------------------------------------------------------------------------
*Estadística
1. Introducción al R.
2. Estadística Descriptiva.
3. Probabilidad.
4. Modelos Probabilísticos.
5. Estimadores. Distribución en el muestreo.6. Intervalos de Confianza.
7. Contraste de hipótesis.
8. Contrastes no paramétricos.
9. Análisis de la Varianza.
10. Regresión Lineal y Correlación.*Cálculo de probabilidades
I. Modelo básico de la Probabilidad
1.- La experiencia del azar
2.- El modelo matemático de la probabilidad
3.- La asignación de probabilidades
4.- Las fórmulas de inclusión-exclusión
5.- Extensiones del modelo matemático
II. La noción de condicionamiento
6.- Probabilidad condicionada
7.- Independencia de sucesos
III. Variables aleatorias. Distribuciones y sus características
8.- Variables aleatorias
9.- Esperanza matemática
10.- Análisis descriptivo de las distribuciones de probabilidad
IV. Las leyes del azar
11.- Pruebas repetidas
12.- Las fluctuaciones del azar*Funciones de una variable
1. Sucesiones de Cauchy y sucesiones convergentes.
2. El cuerpo de los números reales. Axiomas.
3. Límites infinitos. El criterio de Stoltz.4. Topología de la recta real. Punto interior, exterior, frontera, adherente, de acumulación. Conjuntos compactos.
5. Límite de una función en un punto. Propiedades. Cálculo de límites.
6. Funciones continuas. Continuidad en compactos. Continuidad uniforme.
7. Funciones derivables. Cálculo de derivadas.
8. Extremos absolutos. Teoremas de Rolle, de Cauchy y del valor medio. Regla de L'Hôpital.
9. El teorema de Taylor. Extremos relativos. Funciones convexas.
10. Límites superior e inferior de una sucesión. Subsucesiones. Puntos de aglomeración.
11. Series de números reales (I). Series alternadas. Series de términos positivos.
12. Series de números reales (II). Convergencia absoluta y condicional. Reordenaciones.*Lenguaje matemático, conjuntos y números
1. Nociones de lógica
a) Expresiones matemáticas: Proposiciones
b) Conectores lógicos básicos
c) Construcción de nuevas proposiciones
d) Leyes lógicas condicionales
e) Validación de proposiciones
g) Forma clausulada de proposiciones
2. Conjuntos
a) Ideas sobre conjuntos. Predicados
b) Operaciones con conjuntos
c) Algebra de Boole de las partes de un conjunto
d) Producto cartesiano
e) Relaciones
3. Relaciones y aplicaciones entre conjuntos
a) Relaciones entre conjuntos
b) Relación de equivalencia
c) Relación de orden
d) Aplicaciones entre conjuntos
4. Operaciones internas. Estructuras algebraicas
a) Operaciones internas
b) Grupos
c) Anillos
d) Cuerpos
e) Orden y operaciones
f) Homomorfismos
5. Los números naturales y los números enteros
a) Los números naturales
b) Cardinales finitos y conjuntos finitos
c) Conjuntos infinitos
d) Los números enteros e) Máximo común divisor y mínimo común múltiplo
6. Los números racionales y los números reales
a) Los números racionales
b) Los números decimales
c) Insuficiencia de los números racionales
d) El cuerpo de los números reales
e) Intervalos en R
7. Los números complejos
a) Planteamiento del problema
b) Los números complejos. Definición
c) Representación geométrica de los números complejos
d) Forma exponencial de un número complejo
e) Raíces n-ésimas de un número complejo
f) Aplicaciones geométricasCUALQUIER DUDA QUE TE PLANTEES ACERCA DE ESTOS TEMAS PUEDES DECÍRMELA Y ASÍ NOS SERÁ ÚTIL A LOS DOS.
Ángel
el 6/10/17 -
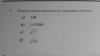
Hola, necesito ayuda con este ejercicio que me pide expresar como potencias los siguientes números, no sé como hacerlo. Gracias por adelantado.
Usuario eliminado
el 27/9/17a) 8 elevado a menos 1
b) -10 elevado a -2
c) 2 elevado a 3/2
d) 16 elevado a 1/3
Cualquier numero elevado a un numero negativo es igual a 1/(Numero elevado al otro numero pero en positivo)
Y cualquier raiz puede escribirse como una potencia si es raiz cuadrada elevado a 1/2 raiz cubica elevado a 1/3 y asi sucesivamente, saludos
Alba
el 27/9/17a)1/8 Primero descomponemos en nº primos los números que se pueda. En este caso el 8 del denominador.
1/2³ : Podrías dejarlo así, o subir el 2³ al denominador cambiando el exponente de signo.
2-³ : Quedaría así.
b) (-1/100) : Al igual que en el anterior, se descompone en nº primos y se sube al denominador.
(-1/5² ·2²) =(5- ² ·2- ²)
c)√2³ : En este caso tenemos una potencia dentro de una raíz. Para transformar la raíz en potencia pasamos el índice de la raíz al denominador del exponente del radicando y quedaría así: 2³¹²
d) ³√16 : En el interior de la raíz tenemos un nº que podemos factorizar como 24 y ahora, como el paso anterior para transformar la raíz en potencia pasamos el índice de la raíz al denominador del exponente del radicando y quedaría así: 24/3
-
Antonio Silvio Palmitano
el 27/9/17Tienes información para tres instantes distintos:
1°)
t = 1s, para el que la posición es: e = 15 m,
luego reemplazas en la ecuación de tu enunciado, y queda:
15 = e0 + v0*1 + (1/2)*a*12,
resuelves coeficientes en cada término, y queda:
15 = e0 + v0 + 0,5*a (1);
2°)
t = 5 s, para el que la posición es: e = 55 m,
luego reemplazas en la ecuación de tu enunciado, y queda:
55 = e0 + v0*5 + (1/2)*a*52,
resuelves coeficientes en cada término, y queda:
55 = e0 + 5*v0 + 12,5*a (2);
3°)
t = 10 s, para el que la posición es: e = 150 m,
luego reemplazas en la ecuación de tu enunciado, y queda:
150 = e0 + v0*10 + (1/2)*a*102,
resuelves coeficientes en cada término, y queda:
150 = e0 + 10*v0 + 50*a (3).
Luego, con las ecuaciones señaladas (1) (2) (3), a las que escribimos con sus miembros permutados, tienes el sistema de tres ecuaciones lineales, de primer grado con tres incógnitas:
e0 + v0 + 0,5*a = 15, de aquí despejas: e0 = 15 - v0 - 0,5*a (4)
e0 + 5*v0 + 12,5*a = 55
e0 + 10*v0 + 50*a = 150;
luego sustituyes la expresión señalada (4) en las otras dos ecuaciones, y queda:
15 - v0 - 0,5*a + 5*v0 + 12,5*a = 55
15 - v0 - 0,5*a + 10*v0 + 50*a = 150;
haces pasajes de términos numéricos y reduces términos semejantes en ambas ecuaciones, y queda
4*v0 + 12*a = 40
9*v0 + 49,5*a = 135;
divides en todos los términos de la primera ecuación por 4, en los de la segunda por 9, y queda:
v0 + 3*a = 10, de aquí despejas: v0 = 10 - 3*a (5)
v0 + 5,5*a = 15;
luego sustituyes la expresión señalada (5) en la última ecuación, y queda:
10 - 3*a + 5,5*a = 15;
haces pasaje de término numérico, reduces términos semejantes, y queda:
2,5*a = 5;
haces pasaje de factor como divisor, y queda:
a = 2 m/s2, que es el valor del módulo de la aceleración del móvil;
luego reemplazas el valor remarcado en la ecuación señalada (5) y queda:
v0 = 10 - 3*2, resuelves, y queda:
v0 = 4 m/s, que es el valor del módulo de la velocidad inicial del móvil;
luego reemplazas los valores remarcados en la ecuación señalada (4) y queda:
e0 = 15 - 4 - 0,5*2, resuelves, y queda
e0 = 10 m, que es el valor del módulo de la posición inicial del móvil.
Luego, reemplazas los valores remarcados en la ecuación del enunciado, resuelves coeficientes, y queda:
e = 10 + 4*t + t2, que es la ecuación de posición del móvil.
Espero haberte ayudado.
-
Di a donde son discontinuas y que tipo de discontinuidad hay
1+x3 / 1+x discontinuidad evitable en x=-1
x2 / x-2 discontinuidad asintotica en x=2
e1/x+1
En este discontinuidad evitable en x=-1
¿Me pueden decir si es correcto?
Ángel
el 27/9/17Lo tienes bien, Ppoblis.
No puedes simplificar y sacar factor común al calcular las discontinuidades (o continuidad) en las funciones racionales, porque obviamente vas "perdiendo una raíz cada vez que le bajas un grado al denominador". EN ESTE CASO NO ES EQUIVALENTE LA FUNCIÓN ORIGINAL Y LA SIMPLIFICADA EN CUANTO CÁCULO DE CONTINUIDAD SE REFIERE.
-
Ayuda, me han explicado de muchas maneras que este determinante es 0, pero de ninguna forma consigo entenderlo. Necesito alguna explicación detallada por favor. Muchas gracias!
Antonius Benedictus
el 27/9/17Una de las propiedades de los determinantes permite sumar a una fila todas las demás. Si le hacemos eso a la primera fila, como el determinante tiene n filas, todos los elementos de la primer fila van a quedar así:
1-n+ (1+1+... (n-1 veces)...+1)=1-n+n-1=0
Y un determinante con una fila de ceros vale 0.