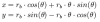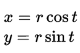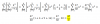-
Usuario eliminado
el 24/9/17El ángulo de elevación de la cúspide de una torre es de 60° a 72 metros de ella, estando el observador a √3 metros sobre el suelo.¿ Cuánto es la altura de la torre?
-
Alisson Ashanty Rojas Cruz
el 24/9/17 -
Gabriel Mondragon
el 24/9/17
Que tal hermanos, estoy haciendo un programa que dibuje un engrane. Los dientes del engrane se generan con una "involuta" y esta debe dejar de dibujarse cuando "toque" el circulo de adendo.
Estoy haciendolo con ecuaciones parametricas y necesito encontrar ese punto de interseccion entre la involuta y el circulo de adendo.
Para la involuta:
Y para el circulo de adendo:
Obviamente tengo que igualar las x con x y Y con Y y me queda un sistema de ecuaciones de la sig forma:
rb*cos(θ)+rb*θ*sin(θ)-r*cos(t)=0
rb*sin(θ)-rb*θ*cos(θ)-r*sin(t)=0Pero este sistema de ecuaciones no lo he podido resolver. El valor que me interesa conocer es el del angulo θ, en funcion de rb y r. Y ni siquiera necesito todos los valores posibles, solo el primero, la primera interseccion.
Si alguien pudiera ayudarme con eso le estaria eternamente agradecido.
Antonius Benedictus
el 24/9/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Ángel
el 24/9/17rb*cos(θ)+rb*θ*sin(θ)-r*cos(t)=0
rb*sin(θ)-rb*θ*cos(θ)-r*sin(t)=0----------------------------------------------------
Sumando ambas ecuaciones:
(1-θ)*(rb*cos(θ)) + (θ-1)*(rb*sin(θ)) -r(cos(t)*sin(t))= 0
Poniendo en función de rb y r la suma de las ecuaciones:
rb*(1-θ)*cos(θ) + rb*(θ-1)*sin(θ) -r(cos(t)*sin(t))= 0
rb[(1-θ)*cos(θ) + (θ-1)*sin(θ)] -r[cos(t)*sin(t)]= 0
rb[(1-θ)*cos(θ) + (θ-1)*sin(θ)] = r[cos(t)*sin(t)]
rb/r = [cos(t)*sin(t)]/ [(1-θ)*cos(θ) + (θ-1)*sin(θ)]
-
Michael Rubio Contrera
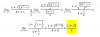
el 24/9/17Buenas me pueden ayudar explicándome como resolver estas desigualdades.
Michael Rubio Contrera
el 24/9/17Michael Rubio Contrera
el 24/9/17Michael Rubio Contrera
el 24/9/17 -
Adrián Sánchez
el 24/9/17 -
Desencadenado
el 24/9/17
Porque teniendo una asintota horizontal en Y=0 la gráfica tiene una raíz en (-1/2;0)?
Antonius Benedictus
el 24/9/17
Antonius Benedictus
el 24/9/17
Ángel
el 24/9/17 -
Usuario eliminado
el 24/9/17 -
Adrián Sánchez
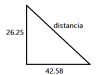
el 24/9/17Hola, tengo este ejercicio de trigonometría y me da 18 kilometros de resultado, podríais echarle un ojo?
Dos vehículos parten de direcciones perpendiculares a velocidades de 45 km/h y 73 km/h respectivamente. ¿Qué distancia les separará al cabo de 35 min?
gracias
-
Agustin Argañaraz
el 24/9/17 -
Agustin Argañaraz
el 24/9/17
