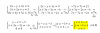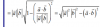-
Hola me podrian ayudar con esta duda ?
¿Todo sistema compatible determinado tiene inversa ?
Antonius Benedictus
el 23/9/17Luis Mplui
el 23/9/17Antonius Benedictus
el 23/9/17 -
Me podrían ayudar con este ejercicio, por favor:
Si f tiene una valor máximo absoluto en 5, entonces f′(5) = 0 .
a. Verdadero
b. Falso
Muchas gracias.
-
 No sabía donde publicar esta duda de estadística (ya que David explica en sus vídeos) lo publicó acá. Es sobre media aritmética, geometríca y armónica... Lo que entiendo es que los datos son 10 y la suma de los precios se divide por 10 para obtener la media Aritmética... Luego con que otra media puedo sacar el promedio?
No sabía donde publicar esta duda de estadística (ya que David explica en sus vídeos) lo publicó acá. Es sobre media aritmética, geometríca y armónica... Lo que entiendo es que los datos son 10 y la suma de los precios se divide por 10 para obtener la media Aritmética... Luego con que otra media puedo sacar el promedio? Por otro lado quería saber cómo desarrollar el punto que sigue. Saludos. Puntos 2 y 3
Antonius Benedictus
el 23/9/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Ángel
el 24/9/171er método: Sumamos todos los precios y lo dividimos por el número de prendas
(5000+12000+3000)/ 10 = 20000/ 10 = 2000
//////////////////////////////////////////////////////////////////////////////////////////////////////////
2º método: Primero obtenemos el promedio de las prendas en cada tienda
5000/2=2500
12000/5=2400
3000/3= 1000
Y después sumamos los promedios con su peso relativo correspondiente (por ejemplo 2/10= 0.2):
2500*0.2= 500
2400*0.5= 1200 +
1000*0.3= 300
------------------ 2000
-
Tengo que resolver este sistema de ecuaciones e interpretar geométricamente los resultados:
3x - 2y = 1
x^2 + y^2 = 25
¿Donde puedo encontrar los videos que me lo expliquen para hacerlo yo?
Saludos
Antonio Silvio Palmitano
el 23/9/17El tema es intersección entre curvas, y en ese caso tienes que la primera ecuación corresponde a una recta, y que la segunda corresponde a una circunferencia con centro en el origen y radio 5.
Observa que puedes tener tres casos:
1°)
La recta y la circunferencia comparten dos puntos, en este caso la recta es secante a la circunferencia.
2°)
La recta y la circunferencia comparten un solo punto, en este caso la recta es tangente a la circunferencia.
3°)
La recta y la circunferencia no comparten puntos, en este caso la recta es exterior a la circunferencia.
Para resolver el sistema, puedes comenzar por hacer pasaje de término en la primera ecuación, y queda:
3x = 1 + 2y, divides por 3 en todos los términos de la ecuación, y queda:
x = 1/3 + 2y/3 (1).
Luego, sustituyes la expresión señalada (1) en la segunda ecuación, y queda:
(1/3 + 2y/3)2 + y2 = 25,
desarrollas el binomio elevado al cuadrado, y queda:
1/9 + 4y/9 + 4y2/9 + y2 = 25,
multiplicas por 9 en todos los términos de la ecuación, y queda:
1 + 4y + 4y2 + 9y2 = 225,
haces pasaje de término, reduces términos semejantes, ordenas términos, y queda:
13y2 + 4y - 224 = 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son:
1°)
y = ( -4-108 )/26 = -112/26 = -56/13 ≅ -4,308,
luego reemplazas en la ecuación señalada (1), y queda:
x = 1/3 + 2*(-56/13)/3 = 1/3 -112/39 = -99/39 = -33/13 ≅ -2,538,
luego, tienes el punto: A( -56/13 , -33/13 );
2°)
y = ( -4+108 )/26 = 104/26 = 4,
luego reemplazas en la ecuación señalada (1), y queda:
x = 1/3 + 2*4/3 = 1/3 + 8/3 = 9/3 = 3,
luego, tienes el punto: B(4,3).
Luego, tienes que el conjunto solución es: S = { A( -56/13 , -33/13 ) ; B(4,3) },
y si representas gráficamente, tienes que la recta es secante a la circunferencia.
Espero haberte ayudado.
-
Hola, como se resuelve el siguiente sistema compatible indeterminado.
2x-y+3z=9
3x+2y+z=3
8x+3y+5z=15
Sé que hay que sustituir una de las variables por Landa, pero luego no se como continuar y ya he visto los vídeos de sistemas compatibles indeterminados, pero como eran con dos ecuaciones no se si se hace de la misma forma. Alguien podría ayudarme a resolverlo?
-
Como se multiplican dos matrices si la matriz A es 2x3 y la matriz B es cuadrada?
Antonio Silvio Palmitano
el 23/9/17Si el orden de los factores es A*B, debe cumplirse que la matriz cuadrada debe ser de orden 3, y la matriz resultado será de dos filas (como la matriz A) y de tres columnas (como la matriz B. Luego, cada elemento de la matriz resultado se calcula como el producto escalar entre "su vector fila" correspondiente en la matriz A, por "su vector columna" correspondiente en la matriz B.
Te recomiendo recurras a los vídeos de Unicoos sobre este tema.
Espero haberte ayudado.
-
Tengo una problema con este ejercicio. El enunciado dice que hay que encontrar el valor de a para que se cumplan las igualdades de los limítes. Uno de ellos es este lim x->∞ (2x-√4x2+ax+1) = 1. Lo que he hecho es igualar a 0 y substituir el valor de la x por 1 en la expresión 4x2+ax+1, pero no me da el resultado.
Antonio Silvio Palmitano
el 23/9/17Observa que el límite es indeterminado, ya que su argumento es una resta de dos términos que tienden a infinito.
Luego, multiplicas y divides por la expresión "conjugada" del denominador, y el argumento del límite queda:
( 2x-(√(4x2+ax+1) )*( 2x+(√(4x2+ax+1) ) / ( 2x+√(4x2+ax+1) ) =
luego, distribuyes en el numerador (observa que tienes cancelaciones de términos opuestos y que te queda una resta de cuadrados perfectos), y queda:
= ( (2x)2 - ( √(4x2+ax+1) )2 ) / ( 2x+√(4x2+ax+1) ) =
resuelves potencias en el numerador, y queda:
= ( 4x2 - (4x2+ax+1) )2 ) / ( 2x+√(4x2+ax+1) ) =
distribuyes el signo en el segundo término del numerador (observa que tienes cancelaciones de términos opuestos), y queda:
= (- ax - 1) / ( 2x+√(4x2+ax+1) ) =
luego divides por x en los dos términos del numerador y en los dos términos del denominador, y queda:
= (- a - 1/x) / ( 2+√(4x2+ax+1)/x ) =
introduces el denominador del segundo término del denominador de la expresión dentro de la raíz cuadrada, lo distribuyes entre los términos de su argumento, y queda:
= (- a - 1/x) / ( 2+√(4+a/x+1/x2) (1).
Luego, pasamos al cálculo del límite que tienes en tu enunciado:
Lím(x→∞) ( 2x-(√(4x2+ax+1) ) =
sustituyes la expresión señalada (1) y queda:
= Lím(x→∞) (- a - 1/x) / ( 2+√(4+a/x+1/x2) =
resuelves (cancelas los términos que tienden a cero) y queda:
= (-a) /( 2+√(4) ) = -a/(2+2) = - a/4;
y como tienes en el enunciado que el límite es igual a uno, plantea:
-a/4 = 1,
multiplicas por -4 en ambos miembros y queda:
a = - 4.
Espero haberte ayudado.
-
Antes de nada felicitaros por vuestro enorme idea! Me encuentro atascado en la simplificación de una solución sobre productos vectoriales. Como se llega de la primera igualación a la segunda?
Gracias!