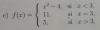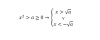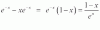-
Jeziel Juarez
el 19/9/17
Buenas unicoos, necesito un poco de ayuda. Tengo una función de transferencia:
Y(s)/X(s) = s.Kd / (1+ s.Td)necesito conocer su salida en forma de ecuación diferencial. Haciendo la transformación de F.T. --> E.D. obtengo la siguiente ecuación:
Td*dy/dt = Kd*dx/dt - y
A partir de allí me encuentro estancado. Supuestamente la siguiente ecuación diferencial es la respuesta que busco,
y' = (Kd/Td^2)*x - (1/Td)*y
pero no logro verificar y comprender los pasos que necesito para llegar a esa solución.
Les agradezco su tiempo y comprensión. Saludos.
Antonius Benedictus
el 19/9/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Santiago Gamboa
el 19/9/17muy buenas unicoos, podrian informarme como desarrollo estos 3 ejercicios?
Ángel
el 19/9/1710.
f(x)=x/(x-1)
P(x1,y1) -----> P(-1,5)
f´(x)= (x-1-x)/(x-1)2= -1/(x-1)2
m=f´(-1)= -1/(-1-1)2 = -1/4
Con los valores que tenemos sustituimos en la punto-pendiente:
y-y1=m(x-x1)
y-5= -1/4(x-(-1))
Manipulamos hasta llegar hasta la ecuación de la recta tangente:
y-5= -1/4(x+1)
y-5= (-1/4)x -1/4
y= (-1/4)x -1/4 +5
y= (-1/4)x +19/4 = mx + n
Santiago Gamboa
el 19/9/17 -
Sarqui
el 18/9/17 -
Santiago
el 18/9/17Hola, podrian ayudarme con este ejercicio?
Encuentre las ecuaciones de las dos rectas tangentes a la elipse x^2 + 4y^2 = 5, que pasen por el punto (-5,0)
gracias de antemano
Antonio Silvio Palmitano
el 19/9/17Puedes comenzar por derivar implícitamente con respecto a x en la ecuación de la elipse, y queda:
2*x + 8*y*y ' = 0, haces pasaje de término, y queda:
8*y*y ' = - 2*x, haces pasajes de factores como divisores, y queda:
y ' = - x(4*y) (1).
Luego, puedes llamar T(a,b) al punto de contacto entre la recta tangente y la elipse.
Luego, como el punto T pertenece a la elipse puedes sustituír sus coordenadas en la ecuación del enunciado, y queda:
a2 + 4*b2 = 5 (2).
Luego, sustituyes las coordenadas del punto T en la expresión de la derivada señalada (1), y tienes una expresión para la pendiente de la recta tangente:
m = - a/(4*b) (3).
Luego, como el punto A(-5,0) pertenece a la recta tangente (observa que no pertenece a la elipse), planteas la ecuación punto-pendiente para dicha recta:
y - 0 = m*( x - (-5) ), cancelas el término nulo, resuelves signos en el agrupamiento, y queda:
y = m*(x + 5), y luego, como el punto de contacto T pertenece a la recta tangente, sustituyes sus coordenadas en la ecuación de la recta, y queda:
b = m*(a + 5) (4).
Luego, con las ecuaciones señaladas (2) (3) (4) tienes el sistema de ecuaciones:
a2 + 4*b2 = 5 (2)
m = - a/(4*b) (3)
b = m*(a + 5) (4).
Luego, sustituyes la expresión señalada (2) en la ecuación señalada (4) y el sistema queda:
a2 + 4*b2 = 5 (2)
b = - ( a/(4*b) )*(a + 5) (5).
Luego, multiplicas por 4*b en ambos miembros de la ecuación señalada (5), y queda:
a2 + 4*b2 = 5 (2)
4*b2 = - a*(a + 5) (5).
Luego, restas miembro a miembro entre las ecuaciones señaladas (2) (5), y queda:
a2 = 5 + a*(a + 5).
Luego, distribuyes en el último término, y queda:
a2 = 5 + a2 + 5*a,
haces pasajes de términos (observa que tienes cancelaciones de términos cuadráticos), y queda:
- 5*a = 5,
haces pasaje de factor como divisor, y queda:
a = - 1.
Luego, reemplazas en las ecuaciones señaladas (2) (5), y qedan:
1 + 4*b2 = 5, aquí haces pasaje de término y queda: 4*b2 = 4
4*b2 = 4,
luego, divides por 4 en ambos miembros de ambas ecuaciones, y quedan:
b2 = 1,
haces pasaje de potencia como raíz, y tienes dos opciones:
1°)
b = - 1, que conduce al punto de contacto: T1(-1,-1),
luego reemplazas los valores remarcados en la ecuación señalada (3) y queda:
m = - (-1)/( 4*(-1) ) = 1/(-4) = - 1/4, que es la pendiente de la recta tangente,
luego planteas su ecuación punto-pendiente:
y - (-1) = - (1/4)*( x - (-1) ), resuelves signos en ambos miembros, distribuyes en el segundo miembro, y queda:
y + 1 = - (1/4)*x - 1/4, haces pasaje de término, y queda:
y = - (1/4)*x - 5/4, que es la ecuación de la recta tangente a la elipse que pasa por el punto A(-5,0) y por el punto de contacto T1(-1,-1).
2°)
b = 1, que conduce al punto de contacto: T2(-1,1),
luego reemplazas los valores remarcados en la ecuación señalada (3) y queda:
m = - (-1)/( 4*1 ) = 1/4, que es la pendiente de la recta tangente,
luego planteas su ecuación punto-pendiente:
y - 1 = (1/4)*( x - (-1) ), resuelves signos en el agrupamiento, distribuyes en el segundo miembro, y queda:
y - 1 = (1/4)*x + 1/4, haces pasaje de término, y queda:
y = (1/4)*x + 5/4, que es la ecuación de la recta tangente a la elipse que pasa por el punto A(-5,0) y por el punto de contacto T2(-1,1).
Espero haberte ayudado.
-
Rosario
el 18/9/17 -
Carlos Sanchez
el 18/9/17 -
Carlos Sanchez
el 18/9/17 -
Valeria C
el 18/9/17Por favor URGENTE me gustaría resolver un problema para mi primo
Carlos paga 450 € mensuales por el alquiler del piso, lo que supone un 30% del sueldo ¿cuánto gana al mes?
Por favor es URGENTE
-
necronomicion00
el 18/9/17Tengo una pequeña duda para las inecuaciones.
Si por ejemplo ahora yo tengo x2>3/2 al pasar el cuadrado cambia el signo de la inecuacion? Me refiero a que si ocurre esto: como tenemos esa inecuacion, al pasar de lado nos queda x > ±√(3/2)
Entonces por un lado nos sale x > + √(3/2) y por otro lado nos sale x < - √(3/2) o símplemente se queda x > - √(3/2). Me gustaría también saber porque ocurre. Gracias
-
lbp_14
el 18/9/17
