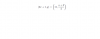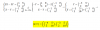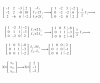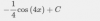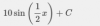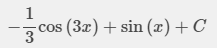Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

lbp_14
el 19/9/17

Hola Unicoos,
No sé si tengo algún error en estos dominios .
Muchas gracias

••0 voto/s
•
César
el 19/9/17

•1 voto/s
•

Cancelar
Carlos Sanchez
el 19/9/17

Considere los siguientes pares ordenados, determine el valor de "x" y de "y" de manera que se
cumpla que:
Hola algún unicoo que me ayude con este ejercicio.

••0 voto/s
•
César
el 19/9/17
2x+1=11
y=(x+3)/2
x=5 y=(5+3)/2=4

•1 voto/s
•

Cancelar
Manuel
el 19/9/17

Hola podeis ayudarme a resolver este ejercicio?

••0 voto/s
•
Antonius Benedictus
el 19/9/17

•1 voto/s
•

Cancelar
Javi Santos
el 19/9/17

Buenas Tardes Unicoos si podeis ayudarme con este limite cuando tiende a +∞ de la función x³-200x. Gracias a vuestra ayuda pude aprovar las mates de 1ro de bachillerato!!!!! :)

••0 voto/s
•
Antonius Benedictus
el 19/9/17
Vale +infinito, pues manda el término de mayor grado.

•0 voto/s
•
Desencadenado
el 19/9/17
Límite infinito menos infinito con raiz cubica
•0 voto/s
•

Cancelar
Alba Sáenz
el 19/9/17

Alguien me puede explicar como resolver este sistema de matrices por pasos

••0 voto/s
•
Antonius Benedictus
el 19/9/17

•1 voto/s
•

Cancelar
fina
el 19/9/17

Quien me puede ayudar con este problema??:
Cuanto tiempo se ha de depositar un capital a un interes compuesto del 8% para que se triplique si la capitalizacion es mensual?

gracias

••0 voto/s
•
Antonius Benedictus
el 19/9/17

•1 voto/s
•

Cancelar
Álvaro
el 19/9/17

¿Alguien sabe resolverme este ejercicio: encuentra dos matrices A y B de dimensión 2 x 2 que cumplan: 2A + B = (1 4 2 0) y A - B = (1 4 2 0)?

••0 voto/s
•
César
el 19/9/17

•0 voto/s
•

Cancelar
Sonia Ramis García
el 19/9/17

Alguien puede realizar este ejercicio? Gracias

••0 voto/s
•
Antonius Benedictus
el 19/9/17
¿En qué nivel educativo estás y dónde, Sonia?

•0 voto/s
•
Sonia Ramis García
el 19/9/17
Es 1ero de Universidad, pero os sigo necesitando please!

•1 voto/s
•
Guillem De La Calle Vicente
el 19/9/17

•3 voto/s
•

Cancelar
JUAN AMPIE
el 19/9/17

Hola buenas tardes quisiera saber si me pudieran revisar este ejercicio y si de paso me ayudan con el otro se los agradeceria mucho

••0 voto/s
•
Ángel
el 19/9/17
El proceso de triangulación de la matríz está bien.

•1 voto/s
•
JUAN AMPIE
el 19/9/17
Muchas gracias, de casualidad me podrias ayudar con el otro ejercicio?

•0 voto/s
•
Ángel
el 19/9/17
En el intento fallido que he hecho:
he sumado las probabilidades de cada columna y cada fila en la tabla HOY/MAÑANA y se obtiene P=1 sumando cada fila y cada columna (CORRECTO)
después he calculado las probabilidades en cada uno de los 9 cuadritos de la tabla HOY/PASADOMAÑANA, PERO obtengo en cada columna y en cada fila sumas diferentes a 1

He pensado en "ajustar" a lo bruto las probabilidades a proporción para que sumen p=1 cada columna y cada fila, pero cuando ajusto una se me descompone otra (¡necesito un método!)...desconozco qué técnicas estás estudiando en clase para afrontar ejercicios similares.
Busca entre tus ejercicios con solución alguno que se le parezca y adjúntalo, porque si no, difícil.

•1 voto/s
•
JUAN AMPIE
el 19/9/17
Es matrices de probabilidad o estocásticas ,Se resuelve supuestamente por cadena de Markov, la verdad me tiene confundido me puedes ayudar por favor?

•0 voto/s
•
Ángel
el 19/9/17
Para la próxima vez, si el tema está fuera de contenido danos las pistas el primer día, no una semana después please!
Cadena de Markov:

•1 voto/s
•
Ángel
el 19/9/17

•1 voto/s
•
Ángel
el 19/9/17
Por ejemplo, el proceso a seguir para sacar el elemento a₁₁ de la matríz 3x3 correspondiente a "Hoy soleado, pasado mañana soleado" es:
Te sitúas en la cadena de Markov y tienes que hacer "viajes" de dos flechas (comenzando en soleado y acabando en soleado). Tienes 3 combinaciones:
Hoy soleado, mañana soleado, pasado mañana soleado= 0.4*0.4
Hoy soleado, mañana nublado, pasado mañana soleado= 0.4*0.3
Hoy soleado, mañana lluvioso, pasado mañana soleado= 0.2*0.1

Si lo sumas obtienes 0.3

•1 voto/s
•
JUAN AMPIE
el 20/9/17
Muchisimas gracias y disculpeme por no dejar mucho detalle es que esta misma pregunta la deje unas 3 veces y nadie me contestaba y no tenia la esperanza que alguien me contestara y eso de lo de markov me dio la idea una persona ya bien noche, Gracias por la explicacion

•0 voto/s
•
Ángel
el 20/9/17
Bueno, dicen por aquí que más vale tarde que nunca...
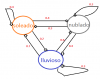
-Te dejo alguna observación acerca de la cadena de Markov obtenida y la "conexión" con el tema de grafos (por si te sirve para la entrega de tu trabajo) :
*En esencia, es una grafo,
*de 3 nodos (soleado, nublado y lluvioso)
*con relación de equivalencia (es reflexiva=cada nodo está relacionado consigo mismo, simétrica=si un nodo está relacionado con uno, ese uno también está relacionado con el otro y transitiva= si el nodo1 está relacionado con el nodo 2 y el nodo 2 con el 3, entonces el nodo 1 está relacionado con el 3)

Si tienes alguna duda me cuentas.

•0 voto/s
•

Cancelar
Alejandro De Jesus Torres Chuna
el 19/9/17

Quien me ayuda? Gracias de antemano.
integrales de Funciones Trigonométricas:

∫x Cos x2dx

∫sen 4x dx

∫5 cos x/2 dx

∫Sen3x . Cos x dx

••0 voto/s
•
Jeziel Juarez
el 19/9/17
1.-
2.-
3.-
4.- Copiaste mal probablemente: Integral (sen 3x + cos x) dx =

•1 voto/s
•
Ángel
el 19/9/17
∫x Cos x²dx = 1/2 ∫2x Cos x²dx= 1/2(sen(x²)) + C = (sen(x²))/2 + C
∫sen 4x dx= 1/4 ∫4sen 4x dx= 1/4(-cos(4x)) +C = -cos(4x))/4 +C
∫5 cos x/2 dx= 5 ∫ cos x/2 dx= 5*2* ∫ 1/2*cos x/2 dx = 10(sen(x/2)) +C
∫Sen3x * Cos x dx = https://es.symbolab.com/solver/step-by-step/%5Cint%20%5Cleft(sen3x%5Ccdot%20cosx%5Cright)dx

•1 voto/s
•

Cancelar