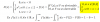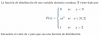Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Guillem De La Calle Vicente
el 22/8/17

Utilice una calculadora o un ordenador para dibujar la función f y, ampliando la gráfica, determine el rango de f con una exactitud de dos cifras decimales.
f(x)=(x-1)/(x²+x)

••0 voto/s
•
Ángel
el 22/8/17
Rango f(x)= ]-∞, 0.17] ∪ [5.83, ∞[

•0 voto/s
•

Cancelar
Laura
el 22/8/17

Un saludo unicoos
algjien podría ayudarme con este ejercicio de mates. Es que no me sale. Seria el siguiente:

••0 voto/s
•
Ángel
el 23/8/17
Datos del enunciado:
P(F)= P(Francés)=14/30= 7/15
P(E)= P(Inglés)=18/30= 3/5
P(F∩E)= 6/30= 1/5  ------> Como la intersección no es cero, son sucesos compatibles

a) Probabilidad de que no haya aprobado ni inglés ni francés= no(Frances y inglés)= P ¬(F ∪ E)
Sabemos que P(F∩E)= 1/5, es distinto de cero, por lo que son sucesos compatibles. La fórmula de la unión sería:
P(F ∪ E)= P(F)+P(E)+P(F∩E) =  7/15+ 3/5 - 1/5 = (7+9-3)/15= 13/15
Ya tenemos el dato de P(F ∪ E)= 13/15 y queremos obtener su complementario o negación: P ¬(F ∪ E) =
P ¬(F ∪ E)+ 13/15 = 1 --------->   P ¬(F ∪ E)= 1- 13/15 = 2/15 es la probabilidad de no aprobar ninguna de las dos asignaturas.

b) P(apruebeingléssabiendoquehaaprobadofrancés)= P(E | F)= P(F∩E) ÷ P(F) = 1/5 ÷ 7/15 = 15/35 = 3/7

•0 voto/s
•

Cancelar
Yajaira Feller Sanchez
el 22/8/17

Hola unicoos,
Alguien podría ayudarme con el apartado B? Es que no me sale lo de añadirle una traslación con el vector...
seria el siguiente enunciado:

El apartado A lo he hecho así, por si sirve de ayuda para el apartado B:

muchas gracias.

••0 voto/s
•
Antonio Silvio Palmitano
el 22/8/17
Simplemente tienes que sustituir x e y por (x-2) e (y-3), respectivamente, en la ecuación final del inciso (a), luego distribuyes, ordenas términos, y extraes factores comunes en los términos con x y en los términos con y.
Te dejo la tarea.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
Stiven
el 22/8/17

Hola, alguien me puede ayudar con derivadas implicitas, llego a un momento en donde no se que hacer., derivar con respecto a x

••0 voto/s
•
Antonius Benedictus
el 22/8/17

•0 voto/s
•
Stiven
el 22/8/17
Muchas gracias por responder, tengo una duda me puedes explicar que operaste para que saliera lo que subraye porfavor.

•0 voto/s
•

Cancelar
Guillem De La Calle Vicente
el 22/8/17

••0 voto/s
•
Antonius Benedictus
el 22/8/17

•0 voto/s
•

Cancelar
Michelle Cardona
el 22/8/17

hola, tengo una duda respecto a ley de senos, cuando se hace el despeje el seno que esta multiplicando y pasa dividiendo se vuelve sen^-1? intenté hacerlo pero mi resultado es diferente
senδ/250=sen120/107.8=senα/150
si pudieran ayudarme por favor, gracias

••0 voto/s
•
Guillem De La Calle Vicente
el 22/8/17
No se entiende tu pregunta, pero simplemente despeja δ y α. En tu ejemplo, no es posible encontrar los valores de δ y α porque cuando despejas te da senδ=x y x>1 y sabes que un seno mayor que 1 no existe.
Saludos.

•0 voto/s
•

Cancelar
Guillem De La Calle Vicente
el 22/8/17

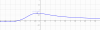
Utilice una calculadora o un ordenador para dibujar la función f y, ampliando la gráfica, determine el rango de f con una exactitud de dos cifras decimales.
f(x)=(x+2)/(x²+2x+3)

••0 voto/s
•
Desencadenado
el 22/8/17

•0 voto/s
•
Guillem De La Calle Vicente
el 22/8/17
Y el rango?

•0 voto/s
•
Desencadenado
el 22/8/17
dom = todos los IR
img = (0 ; 0.68)

•0 voto/s
•
Usuario eliminado
el 22/8/17
[-0.18,0.68]

•0 voto/s
•
Antonio Silvio Palmitano
el 22/8/17
Vamos con una orientación, para la determinación del rango de la función.
Plantea:
y = f(x), sustituyes la expresión de la función en el segundo miembro y queda:
y = (x+2)/(x²+2x+3), haces pasaje de divisor como factor y queda:
y*(x²+2x+3) = x+2, distribuyes en el primer miembro y queda:
y*x² + 2y*x + 3y = x + 2, haces pasajes de términos, extraes factor común en los términos lineales para x y queda:
y*x² + (2y - 1)*x + (3y - 2) = 0, que es una ecuación polinómica cuadrática para x, cuyo discriminante queda:
D = (2y - 1)² - 4y*(3y - 2), desarrollas y queda:
D = 4y² - 4y + 1 - 12y² + 8y, reduces términos semejantes y queda:
D = - 8y² + 4y + 1.
Luego, solo quedas que plantees la condición: D ≥ 0, para que la ecuación admita soluciones reales,
y a partir de allí podrás obtener el rango de la función.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Laura Viñuela
el 22/8/17

¿me podéis ayudar con este problema?:
Dada la recta r que pasa por (1,5)y (4,-1)calcula la distancia a la recta s: 2x+y=-1

••0 voto/s
•
Guillem De La Calle Vicente
el 22/8/17

•1 voto/s
•

Cancelar
Guillem De La Calle Vicente
el 22/8/17

••0 voto/s
•
Antonius Benedictus
el 22/8/17

•1 voto/s
•

Cancelar
Adrián Rodriguez Machuca
el 22/8/17

sabiendo que cos∝= 4/5 y que 0<∝<π/2
halla sen∝, cos∝,tg (180 - ∝) y sen (-∝)

••0 voto/s
•
Guillem De La Calle Vicente
el 22/8/17

•0 voto/s
•

Cancelar