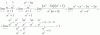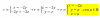Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Nico
el 15/8/17

hola buenas tardes me podrian ayudar con este ejercicio?

••0 voto/s
•
Aguilar Garcia
el 15/8/17
Hola Antonio , me podrías ayudar con el problema que acabo de subir? , esta muy difícil y creo que imposible

•0 voto/s
•
Aguilar Garcia
el 15/8/17

•0 voto/s
•

Cancelar
Luis Alfredo Pinto
el 15/8/17

••0 voto/s
•
Ángel
el 15/8/17
https://www.unicoos.com/video/matematicas/4-eso/probabilidad/probabilidad-condicionada/probabilidad-total-diagrama-de-arbol
https://www.unicoos.com/video/matematicas/4-eso/probabilidad/probabilidad-condicionada/teorema-de-bayes

•0 voto/s
•

Cancelar
Sebastián
el 15/8/17

hola, alguie me podria ayudar a resolver este problema...

Muchas gracias!.

••0 voto/s
•
Ángel
el 15/8/17

•0 voto/s
•
Ángel
el 15/8/17
Hay un error que se repite en lo que te envié: cambia en todos los pasos la expresión x²+y²≤ √2 por x²+y²≤ (√2)²

•0 voto/s
•

Cancelar
Joship
el 15/8/17

Hola quería corroborar lo hecho por mi desarrollo, de ante manó gracias al que me ayude saludos

••0 voto/s
•
Ángel
el 15/8/17
La b si haces (5.5)^0 =1 , no es igual a 50 (como dice el enunciado), luego esa opción la descartamos.
Las 3 últimas las puedes descartar también, porque log0 no existe .

El apartado a) es el correcto porque cumple la condición inicial y las sucesivas:
t(0)=50*(1.1)^0 = 50*1= 50
t(1)=55
t(2)=60.5
.
.
t(x)=50*(1.1)^x

Es correcto tu desarrollo.

•1 voto/s
•

Cancelar
Emilio Ramos Sorroche
el 15/8/17

Hola
Sguramente no es el mejor sitio para esto, pero no he encontrado un e-mail o formulario de contacto
Quisiera informar al webmaster/s de que justo hoy se os caducado el certificado de la página web unicoos.com por lo que algunos navegadores ni si quiera dejan acceder y otros dan fallos de seguridad impidiendo el correcto seguimiento de las lecciones.
Espero que lo podáis solucionar pronto
Un saludo

••1 voto/s
•
Ángel
el 15/8/17

•0 voto/s
•
Ángel
el 15/8/17
Por si sirve a los de soporte:
Windows: https://support.microsoft.com/es-es/help/931850/-there-is-a-problem-with-this-website-s-security-certificate-when-you
Linux: https://nessys.es/go/knowledgebase.php?action=displayarticle&id=60

•0 voto/s
•

Cancelar
Cristina Cris Silka
el 15/8/17

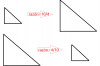
En semejanza cuando tengo que calcular la razón= a/a´=b/b´=c/c´siempre el número más grande va arriba porque sino me daría una razón fraccionaria, por ej: r=10/4 =5/2 ó r= 4/10= 2/5 ?

••0 voto/s
•
Rouché
el 15/8/17
Hola Cristina
La razón va a estar bien si colocas el número mayor en el numerador o en el denominador. Por ejemplo 1/2 la razón podría ser 0.5 ( donde el todo va a ser la unidad) o también 2.
Un saludo

•1 voto/s
•
Ángel
el 15/8/17
El número más grande puede estar arriba o abajo indistintamente, no es una condición el que tenga que estar en un lado u otro.
Todo dependerá de si el triángulo original es más pequeño o más grande

•1 voto/s
•
Cristina Cris Silka
el 16/8/17
Muchas gracias!!!

•0 voto/s
•

Cancelar
Rouché
el 15/8/17

Una ayudita con el ejercicio 50 por favor.
Lo he intentado hacer con Pitágoras pero no me sale...

••0 voto/s
•
Antonius Benedictus
el 15/8/17

•0 voto/s
•

Cancelar
Rouché
el 15/8/17

En Geometría analítica, que coordenadas tiene el denominado 'plano horizontal'?
Es x=O ??

••0 voto/s
•
Antonius Benedictus
el 15/8/17
El plano OXY tiene por ecuación x=0.

•0 voto/s
•

Cancelar
Sonia Ramis García
el 15/8/17

Hola. No entiendo cómo se encuentra el numero que multiplica n2(n2 + 1). Un poco de luz a esto?

••0 voto/s
•
César
el 15/8/17
Puedews hacerlo asi

•0 voto/s
•
Antonio Silvio Palmitano
el 15/8/17
Vamos con una orientación para tu consulta, y con una forma alternativa para resolver el límite, que podría ser útil.
Comienza por tomar denominador común en el numerador (N) del argumento del límite:
N = 1/n - 3/n² = extraes denominador común = (n - 3)/n².
Tienes el denominador (D) del argumento del argumento del límite:
D = (n + 1)/(n² + 1).
Luego, tienes el límite:
Lím(n→+∞) [ 1/n - 3/n² ] / [ (n + 1)/(n² + 1) ] =
sustituyes en el numerador y queda:
= Lím(n→+∞) [ (n - 3)/n² ] / [ (n + 1)/(n² + 1) ] =
( observa que el factor que introducen en tu enunciado es el mínimo común múltiplo entre los denominadores remarcados, que en este caso es su producto: n²*(n² + 1) ).
resuelves la división entre expresiones fraccionarias y queda:
= Lím(n→+∞) [ (n - 3)*(n² + 1) / n²*(n + 1) ] =
distribuyes en el numerador y en el denominador y queda:
= Lím(n→+∞) [ n³ - 3n² + n - 3 ] / [ n³ + n² ] =
extraes factores comunes en el numerador y en el denominador, según los términos de mayor grado, y queda:
= Lím(n→+∞) [ n³*(1 - 3/n + 1/n² - 3/n³) ] / [ n³*(1 + 1/n) ] =
simplificas los factores comunes y queda:
= Lím(n→+∞) [ 1 - 3/n + 1/n² - 3/n³ ] / [ 1 + 1/n ] =
resuelves y queda:
= [ 1 - 0 + 0 - 0 ] / [ 1 + 0 ] = 1 / 1 = 1.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Rouché
el 15/8/17

Hola! Una pregunta súper rápida de geometría, que me ha dejado atascada :
una recta con la forma : x=-2y=-2z
Cómo puedo sacar sus ecuaciones paramétricas?
muchas gracias!

••0 voto/s
•
Antonius Benedictus
el 15/8/17

•0 voto/s
•

Cancelar