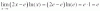-
Martin A. Garcia
el 16/8/17buenas tengo una consulta quiero resolver un ejercicio en el cual no puedo realizar es: lim x--> e [(2x-e) . lnx ]
Ángel
el 16/8/17 -
Jordi García
el 16/8/17 -
Sergi
el 16/8/17
Jordi García
el 16/8/17Hola Sergi,
Si han necesitado 10 días trabajando 12 horas diarias para fabricar 600 coches, han trabajado en total 10 * 12 = 120 horas para fabricarlos.
Con una regla de tres lo resolvemos:
120 h → 600 coches
x h → 200 coches
Entonces, 120/x = 600/200 → x = (120 * 200) / 600 = 40 h
Si tardan 40 h, trabajando 8 horas diarias tardarán 40 / 8 = 5 días
Espero haberte ayudado.
Saludos.
-
Ryan Benitez
el 16/8/17Me pueden ayudar a encontrar el valor de "k" en estas ecuaciones de rectas?
Las dos rectas 2y-9kx+2=0, 1/2y-x/k-1=0, son paralelas, entonces aplicando los conceptos básicos de pendientes de rectas ¿Cual es el valor de "k"?
Antonio Silvio Palmitano
el 16/8/17Observa que cuando tienes ecuaciones cartesianas implícitas de rectas:
ax + by + c = 0
Ax + By + C = 0,
puedes plantear para la condición de paralelismo en la forma:
a/A = b/B (1) y a/A = c/C (2).
Luego, según tu enunciado, tienes las ecuaciones (observa que ordenamos términos):
- 9kx + 2y + 2 = 0, por lo que aquí tienes: a = -9k, b = 2, c = 2;
(-1/k)x + (1/2)y - 1 = 0, por lo que aquí tienes: A = -1/k, B = 1/2, C = -1.
Luego sustituyes en las ecuaciones señaladas (1) (2) y quedan:
-9k / (-1/k) = 2 / (1/2)
-9k / (-1/k) = 2 / (-1),
resuelves en ambos miembros de ambas ecuaciones y queda:
9k2 = 4
9k2 = - 2, aquí haces pasaje de factor como divisor y queda: k2 = - 2/9, haces pasaje de potencia como raíz y queda: k = √(-2/9) ∉ R,
por lo que tienes que las rectas cuyas ecuaciones tienes en el enunciado no son paralelas, para todo valor real k.
Por favor, verifica que hayas transcrito bien las ecuaciones en tu enunciado, y si están correctamente escrita, consulta con tu docentes, porque puede haberse deslizado algún error.
Espero haberte ayudado.
-
Jocelyn J
el 16/8/17 -
jorge velazquez
el 16/8/17Demuestre:
Sea x elemento de los reales,
Si x>5 entonces x>3
Usa el método ddemostración directo
Ángel
el 16/8/17
Antonio Silvio Palmitano
el 16/8/17Vamos con un desarrollo.
Observa que tienes la Hipótesis: x > 5.
Observa que para todo x real se cumple: x > x - 2 (1).
Luego, partes desde la Hipótesis:
x > 5, restas 2 en ambos miembros (por propiedad uniforme de la resta) y queda:
x - 2 > 3 (2).
Luego, tienes las desigualdades señaladas (1) y (2):
x > x - 2 y x - 2 > 3,
luego, por transitividad de la relación de orden estricto "mayor que" tienes:
x > 3.
Por lo tanto, puedes concluir que la proposición:
x>5 → x>3
es Verdadera, para todo x real.
Espero haberte ayudado.
-
Guillem De La Calle Vicente
el 16/8/17 -
Florencia López
el 15/8/17
-
Aguilar Garcia
el 15/8/17Hola buenas tardes a todos , necesito ayuda urgente con dos problemas no se como hacerlos llevo harto rato pensando es asi
1. demostrar que 1/7Λ1! + 1/7Λ2! + 1/7Λ3! + ......+ 1/7Λn! + ...... es irracional
alguien que sepa hacer este difícil problema ?
2. En una superficie cilindrica en el espacio se encuentra un punto 'P' y existen dos puntos distintos 'A' y 'B' , encontrar cierto punto 'P' talque la suma de los segmentos AP y PB sea minima , los puntos estan en el espacio NO en la superficie
Son imposibles por favor amigos unicoos ayuda
Ángel
el 16/8/17Ejercicio 1.
Es un número de Liouville, que por definición es irracional.
