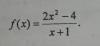-
Un estudiante está resolviendo un examen de tipo test con cuatro respuestas posibles por pregunta. La probabilidad de que realmente sabe la respuesta de una pregunta es 1/3. Cuando el estudiante no sabe la respuesta, elige uno al azar de 4.
Dada una pregunta específica, ¿cuál es la probabilidad de que el estudiante responda correctamente? -
Indique qué simetría (si es que existe alguna) tiene la gráfica de f(x). En particular ¿es f par o impar?
1. f(x)=1/(x²-1)
2. f(x)=1/(x-2)
3. f(x)=1/(x+4)
Ángel
el 17/8/17f(-x)= f(x) ---->PAR
f(-x)= -f(x) ----->IMPAR
1.
f(x)=1/(x²-1)
f(-x)=1/[(-x)²-1)]= 1/(x²-1)
Luego, f(-x)= f(x) ---->PAR --> Simétrica con respecto al eje Y
2.
f(x)=1/(x-2)
f(-x)= 1/(-x-2)= -1/(x+2)
-f(x)= -1/(x-2)
Como -1/(x+2) ≠ 1/(x-2) y -1/(x+2) ≠ -1/(x-2), entonces no es par ni impar
Es simétrica respecto a x=2
Es la función 1/x desplazada dos unidades a la derecha en el eje X
3.
f(x)=1/(x+4)
f(-x)= 1/(-x+4)=
-f(x)= -1/(x+4)
Como 1/(-x+4) ≠ 1/(x+4) y 1/(-x+4) ≠ -1/(x+4), entonces no es par ni impar
Es simétrica respecto a x= -4
Es la función 1/x desplazada cuatro unidades a la izquierda en el eje X
-
Guillem De La Calle Vicente
el 17/8/1718 /1 = 18 monedas de 1 euro
7.20 / 0.1 = 72 monedas de 10 centimos de euro
4.95 / 0.05 = 99 monedas de 5 centimos de un euro
Ahora dice que cuantos amigos han participado como maximo, esto lo hallas con el MCD entre esos tres numeros, que es 9
entonces lo que puso cada uno fue
18/9 = 2 monedas de 1 euro
72/9 = 8 monedas de 10 centimos de euro
99/9 = 11 monedas de 5 centimos de euro -
Ángel
el 17/8/17Antonio Silvio Palmitano
el 17/8/17Llamemos:
x: cantidad total de alumnos,
n: cantidad de alumnos con calificación notable (observa que tienes: n = 45),
f: a la fracción de alumnos que ha obtenido calificación notable (observa que tienes: f = 1/5).
Luego, plantea al ecuación correspondiente a la fracción de alumnos que obtuvo calificación notable:
f = n/x, haces pasaje de divisor como factor y queda:
x*f = n, haces pasaje de factor como divisor y queda:
x = n/f,
reemplazas valores y queda:
x = 45/(1/5) = 45*5 = 225 alumnos.
Espero haberte ayudado.
-
Ángel
el 17/8/17Antonio Silvio Palmitano
el 17/8/17Puedes llamar:
W, al trabajo que se debe realizar,
x: a la velocidad de trabajo de Juan (que tarda: t = 6 min en preparar los obsequios, el solo),
y: a la velocidad de trabajo de Pedro (que tarda: t = 12 min en preparar los obsequios, él solo),
Luego puedes llamar:
x+y: a la velocidad de trabajo de los chicos en conjunto,
T: al tiempo que tardan en realizar el trabajo si lo hacen juntos.
Luego puedes plantear:
W = x*6 (la tarea la realiza solo Juan), haces pasaje de factor como divisor y queda: W/6 = x (1)
W = y*12 (la tarea la realiza solo Pedro), haces pasaje de factor como divisor y queda: W/12 = y (2)
W = (x + y)*T, distribuyes en el segundo miembro y queda: W = x*T + y*T (3).
Luego sustituyes las expresiones señaladas (1) (2) en la ecuación señalada (3) y queda:
W = (W/6)*T + (W/12)*T, multiplicas por 12 en todos los términos de la ecuación y queda:
12*W = 2*W*T + W*T, divides por W en todos los términos de la ecuación y queda:
12 = 2*T + T, reduces términos semejantes en el segundo miembro y queda:
12 = 3*T, haces pasaje de factor como divisor y queda:
4 = T.
Por lo que tienes que el tiempo que tardan los dos chicos trabajando juntos es:
T = 4 minutos,
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 17/8/17Vamos con una orientación.
Tienes una función cuyo dominio es: D = (-∞,-1) u (-1,+∞),
y cuya expresión es una fracción algebraica, y observa que su numerado es de grado 2 y que su denominador es de grado
1, por lo que puedes efectuar la división por medio de la Regla de Ruffini, y obtendrás:
que el cociente es el polinomio: C(x) = 2x - 2, y que el resto es: R = - 2.
Luego, puedes reescribir la expresión de la función:
f(x) = ( 2x2 - 4 ) / (x + 1) = ( (2x - 2)*(x + 1) - 2 ) / (x + 1),
distribuyes el denominador, simplificas en el primer término y queda:
f(x) = 2x - 2 - 2/(x + 1), que es la forma estándar para esta función.
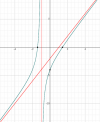
Luego, pasemos al estudio asintótico:
Observa que cuando x tiende a -infinito, tienes que el tercer término tiende a cero,
y que la expresión conformada por los dos primeros términos tiende a - infinito,
Observa que cuando x tiende a +infinito, tienes que el tercer término tiende a cero,
y que la expresión conformada por los dos primeros términos tiende a +infinito,
por lo tanto, tienes que la recta cuya ecuación es:
y = 2x - 2,
es una asíntota oblicua de la gráfica de la función.
Observa que cuando x tiende a - 1 tanto por izquierda como por derecha,
tienes que el tercer término tiende a + infinito (por izquierda) y tiende a - infinito (por derecha),
y que la expresión conformada por los dos primeros términos tiende a - 4,
por lo tanto, tienes que la recta cuya ecuación es:
x = - 1,
es una asíntota vertical de la gráfica de la función.
Espero haberte ayudado.
-
Guillem De La Calle Vicente
el 17/8/17https://es.wikipedia.org/wiki/Deducci%C3%B3n_del_m%C3%B3dulo_de_la_suma
Sustituye en la última fórmula sabiendo que el módulo de los vectores es 1 (porque son unitarios) i el módulo de la suma es raíz de 3, y encuentras el ángulo.
Saludos.
Antonio Silvio Palmitano
el 17/8/17Tienes el módulo de la suma de los dos vectores:
|u + v| = √(3), haces pasaje de potencia como raíz y queda:
|u + v|2 = 3, aplicas la expresión del cuadrado del módulo de un vector como producto escalar:
(u + v) • (u + v) = 3, distribuyes el producto escalar y queda:
u•u + u•v + v•u + v•v = 3, desarrollas los productos escalares y queda:
|u|*|u|*cos0° + |u|*|v|*cosα + |v|*|u|*cosα + |u|*|u|*cos0° = 3,
reemplazas los valores de los módulos y queda:
1*1*cos0° + 1*1*cosα + 1*1*cosα + 1*1*cos0° = 3,
resuelves en cada término y queda:
1 + cosα + cosα + 1 = 3, reduces términos semejantes, haces pasaje de término y queda:
2*cosα = 1, haces pasaje de factor como divisor y queda:
cosα = 1/2, compones en ambos miembros con la función inversa del coseno y queda:
α = 60°.
Espero haberte ayudado.
-
Buenas tengo una duda con esta derivada, muchas gracias de antemano
f(x)= x2-6x-4 en [1,3]
Antonio Silvio Palmitano
el 17/8/17Observa que tienes una función continua, cuyo dominio es un intervalo cerrado.
Luego, por reglas de derivación, separas en términos, derivas término a término, y la expresión de la función derivada queda:
f ' (x) = 2x - 6*1 - 0 = 2x - 6,
pero observa que su dominio es el intervalo abierto: ]1,3[,
y en los extremos solo existen algunas derivadas laterales: por derecha en x = 1, y por izquierda en x = 3.
Espero haberte ayudado.