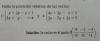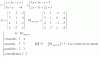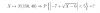-
Ignacio
el 18/8/17
Tengo bien los siguientes resultados del ejercicio?:a.1) Dom(f(x))=(-inf.,0)
a.2) crece (0,1/e^2] u [1, +inf.)
decrece [1/e^2,1]
a.3) Máx. (1/e^2, 0.5413...)
Mín. (1,0)
¿Cómo termino la última parte de este apartado?
César
el 18/8/17
Ignacio
el 18/8/17 -
Daniel Pineda
el 18/8/17Buenas tardes, tengo una duda concreta acerca de una integral impropia: integral de 0 a + infinito de ((sen(x))^2)/(x^2) dx , he encontrado varias soluciones por internet y en todas ellas afirma que el caracter de esa integral impropia es el mismo que el de la integral impropia : integral de 1 a + infinito de ((sen(x))^2)/(x^2) dx. ¿ Alguien me puede explicar por que tienen ambas el mismo carácter ?
Muchísimas Gracias.
-
eva
el 18/8/17Hola,me podéis ayudar
Considera el triángulo isósceles ABC.Los vértices de lado desigual son A(-2,3) i B(2,-1).Encuentra el 3r vértice,sabiendo que la altura del triángulo es el doble del lado AB.
He calculado la distancia AB y me da 2√5, luego lo he multiplicado por su doble. También he calculado el punto media del lado AB y me da Pm(0,-2).
Para calcular el vértice C, considero q es la distancia al punto medio al calcularlo me quedan 2 incógnitas que son las componentes del vértice C, y aquí me quedo bloqueada.
Gracias de antemano
-
Guillem De La Calle Vicente
el 18/8/17En una asamblea universitaria el 4% de los alumnos asistentes son de primer curso, el 9% son de segundo, el 41% son de tercer y el 46% son de cuarto. Hoy se discuten problemas de asignaturas de primer y tercer cursos y el 88% de los alumnos asistentes de tercer han intervenido en la asamblea igual que un 4% de los asistentes de segundo, un 4% de los de cuarto y un 10% de los de primer . Tomamos un alumno al azar que ha intervenido. ¿Cuál es la probabilidad de que sea de tercer curso?
Ángel
el 18/8/17P(Asistenteprimer)=0.04
P(Asistentesegundo)=0.09
P(Asistentetercero)=0.41
P(Asistentecuarto)=0.46
P(intervenidoprimero)= 0.04*0.1= 0.004
P(intervenidosegundo)= 0.09*0.04= 0.0036
P(intervenidotercero)= 0.41*0.88= 0.3608
P(intervenidocuarto)= 0.46*0.04= 0.0184
P(Asistente&intervenidoTercero)= 0.3608/(0.004+0.0036+0.3608+0.0184)= 0.3608/0.3868= 0.9327
-
Laura Viñuela
el 18/8/17 -
Irene AG
el 18/8/17 -
Montserrat Sas
el 18/8/17como se calcula el dominio de funciones? aquí teneis el problema del examen que no sé como se resuelve
gracias
Ángel
el 18/8/17
Antonio Silvio Palmitano
el 18/8/17Tienes las expresiones de dos funciones, de las que indicamos sus dominios:
f(x) = √(x2 - 4), cuyo dominio es (observa que debe cumplirse |x| ≥2): Df = (-∞,-2] u [2,+∞);
g(x) = x2 + 4, cuyo dominio es: Dg = (-∞,,+∞,).
Luego, pasamos a las expresiones de las composiciones, y recuerda que el dominio de la función compuesta debe estar incluido en el dominio de la primera función de la composición por lo que, a lo sumo, puede ser igual al dominio de la primera función:
1)
(g o f)(x) = g( f(x) ) = g( √(x2 - 4) ) = ( √(x2 - 4) )2 + 4 = |x2 - 4| + 4 = (*) = x2 - 4 + 4 = x2,
y su dominio es: Dgof = Df = (-∞,-2] u [2,+∞).
(*) Observa que el argumento del valor absoluto es positivo para todo elemento del dominio de la función f.
2)
(f o g)(x) = f( g(x) ) = f(x2 + 4) = √( (x2 + 4)2 - 4 ),
y observa en el argumento de la raíz que el primer término (cuyo valor mínimo es: 42 = 16) es mayor que el segundo
término, por lo que tienes que la expresión está definida para todo elemento del dominio de la función g,
y el dominio de esta función compuesta es: Dfog = (-∞,+∞).
Espero haberte ayudado.
-
Usuario eliminado
el 18/8/17 -
Juanita
el 18/8/17Hola, quisiera ayuda con este ejercicio:
Se desea recargar el cajero de un banco con billetes de 10, 20 y 50 euros. Por cada 5 billetes de 50 se ha de introducir 1 de 20, mientras que por cada 2 billetes de de 20 se han de introducir 3 de 10.
-Plantear un sistema de ecuaciones para determinar la proporción de cada una de las denominaciones de billetes que hay que introducir en el cajero.
-Si el importe total en euros de todos los billetes ha de ser 38500 euros ¿Cuantos billetes de cada denominación hay que introducir en el cajero?
No se como hacer para poder plantearlo de alguna manera para resolverlo mediante la regla de Cramer.
Gracias. Sólo con saber que proceso debo llevar a cabo, estaría muy feliz :)
-
Nacho
el 18/8/17hola alguien me da una mano, especialmente en la parte de hallar "t"
no entiendo como plantear la paralela al eje z
Antonio Silvio Palmitano
el 18/8/171°) Para determinar las coordenadas del punto de intersección de la recta r con la recta s, sustituyes las expresiones de x, y, z en función del parámetro λ en las ecuaciones cartesianas de la recta s, y queda el sistema de dos ecuaciones con una incógnita:
(2+λ) - (1-2λ) + (5+λ) = - 10
(2+λ) - (1-2λ) = - 11,
distribuyes los agrupamientos y reduces términos semejantes en ambas ecuaciones, haces pasajes de términos y queda:
4λ = - 16
3λ = - 12,
y observa que en ambas ecuaciones despejas:
λ = - 4,
luego reemplazas en las ecuaciones cartesianas paramétricas de la recta r y queda:
x = 2 + (- 4) = 2 - 4 = - 2,
y = 1 - 2(- 4) = 1 + 8 = 9,
z = 5 + (- 4) = 5 - 4 = 1,
por lo que tienes que el punto de intersección entre las rectas r y s tiene coordenadas:
A(-2,9,1),
y las ecuaciones cartesianas de la recta t, que es paralela al eje coordenado OZ que pasa por este punto son:
x = - 2
y = 9.
Luego, plantea las componentes del vector normal al plano π por medio del producto vectorial:
n = PQ x PR = <-1-2,2-1,1-0> x <0-2,5-1,-2-0> = <-3,1,1> x <-2,4,-2> = <-6,-8,-10>,
luego, plantea la ecuación cartesiana del plano π, a partir de las coordenadas del punto P y de las componentes del vector normal n:
- 6(x - 2) - 8(y - 1) - 10(z - 0) = 0,, distribuyes, reduces términos numéricos, haces pasaje de término y queda:
- 6x - 8y - 10z = - 20, divides en todos los términos de la ecuación por - 2 y queda:
3x + 4y + 5z = 10.
Luego, plantea la intersección de la recta t con el plano π por medio del sistema de ecuaciones:
x = - 2
y = 9
3x + 4y + 5z = 10,
reemplazas los valores remarcados en la última ecuación y queda:
3(- 2) + 4(9) + 5z = 10, resuelves términos, reduces términos semejantes, haces pasaje de término y queda:
5z = - 20, haces pasaje de factor como divisor y queda:
z = - 4,
por lo que tienes que la recta t y el plano π se cortan en el punto cuyas coordenadas son:
B(-2,9,-4).
Espero haberte ayudado.
