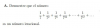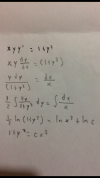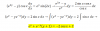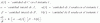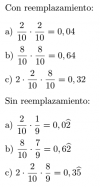-
Hola unicoos , si tengo un P y Q numeros distintos y enteros positivos entonces al momento de igualar P/Q = ∑ desde n=1 hasta un K de (1/7Λn!) , puedo decir que Q= 7Λk! ?? alguien me puede explicar ?
Antonius Benedictus
el 17/8/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Antonio Silvio Palmitano
el 17/8/17Tienes la sumatoria:
∑(n=1,k) (1/7n) = ∑(n=1,k) (1/7)n =
observa que es una suma geométrica cuya razón es q = 1/7 < 1, por lo que su resultado es:
= (1/7)*(1 - (1/7)k)/(1 - 1/7) =
resuelves el divisor y queda:
= (1/7)*(1 - (1/7)k)/(6/7) =
resuelves la división entre el primer factor y el divisor, y queda:
= (1/6)*(1 - (1/7)k) =
distribuyes la potencia en el segundo término del segundo factor y queda:
= (1/6)*( (7k - 1)/7k ) =
resuelves el producto de expresiones fraccionarias y queda:
= (1*( (7k - 1) ) / (6*7k) =
resuelves el producto en el numerador y queda:
= (7k - 1) / (6*7k) = P/Q,
y tienes que los números enteros que componen la fracción resultado son:
P = 7k - 1,
Q = 6*7k.
Espero haberte ayudado.
-
Axel Morales Piñón.
el 17/8/17Antonio Silvio Palmitano
el 17/8/17Debes corregir en el segundo miembro en la anteúltima línea de tu desarrollo a fin de corregir el procedimiento, que queda:
(1/2)*ln(1+y2) = ln(|x|) + c, multiplicas por 2 en todos los términos de la ecuación y queda:
ln(1+y2) = 2*ln(|x|) + 2*c, aplicas la propiedad del logaritmo de una potencia en el primer término del segundo miembro, renombras a la constante arbitraria 2*c y queda:
ln(1+y2) = ln(x2) + ln(C), aplicas la propiedad del logaritmo de un producto en el segundo miembro y queda:
ln(1+y2) = ln(C*x2), compones en ambos miembros con la función inversa del logaritmo natural y queda:
1+y2 = C*x2, que es una solución general implícita de la ecuación diferencial de tu enunciado.
Espero haberte ayudado.
-
Hola,Unicoos,me ayudarian con esto? Gracias de antemano!
Se disponen de 30 vacas de la raza Holando y 35 de la raza Criolla en un mismo lote.Si se extraen simultaneamente dos vacas al azar,cual es la probabilidad de que:
a) ambas sean Holando
b)Sean de la misma raza
c)Sean de distinra raza
d)La primera sea Holando y la segunda Criolla
e)La primera sea Holando
f) La segunda sea Holando,dado que la primera fue criolla.
-
Hola, necesito ayuda con este ejercicio de Geometría Analítica, sólo he llegado a hacer la completación de cuadrados y no sé cómo seguir. Gracias.
Hallar las ecuaciones de las rectas tangentes a la circunferencia x^2+y^2-6x-4y+12= 0 trazadas desde el punto (0,1).
Solución: y=1 ; y=3/4x+1
Antonio Silvio Palmitano
el 17/8/17Tienes la ecuación cartesiana implícita de la circunferencia:
x2 + y2 - 6x - 4y + 12 = 0 (1),
Puedes plantear la ecuación cartesiana de una recta que pasa por el punto de coordenadas A(0,1):
y = mx + 1 (2).
Luego sustituyes la expresión señalada (2) en la ecuación señalada (1) y queda:
x2 + (mx + 1)2 - 6x - 4(mx + 1) + 12 = 0, desarrollas el segundo término y el cuarto término, y queda:
x2 + m2x2 + 2mx + 1 - 6x - 4mx - 4 + 12 = 0, agrupas términos semejantes según x, y queda:
(1 + m2)x2 - 2(m + 3)x + 9 = 0, que es una ecuación polinómica cuadrática para la incógnita x, cuyas soluciones quedan:
x = ( 2(m + 3) ± √(4(m+3)2 - 4*(1 + m2)*9) ) / [2(1 + m2)].
Luego plantea la condición para que tenga única solución (observa que sería la abscisa del punto de contacto entre la circunferencia y la recta tangente):
4(m+3)2 - 4*(1 + m2)*9 = 0, divides por 4 en todos los términos de la ecuación, ordenas factores en el segundo término, y queda:
(m + 3)2 - 9*(1 + m2) = 0, desarrollas el binomios elevado al cuadrado, distribuyes el segundo término, y queda:
m2 + 6m + 9 - 9 - 9m2 = 0, reduces términos semejantes (observa que tienes cancelaciones, ordenas términos, y queda:
- 8m2 + 6m = 0, extraes factor común y queda:
- 2m*(4m - 3) = 0, luego, por anulación de un producto, tienes dos opciones:
a)
- 2m = 0, haces pasaje de factor como divisor y queda:
m = 0, que conduce a la recta cuya ecuación es: y = 0x + 1, cancelas el término nulo y queda: y = 1;
b)
4m - 3 = 0, haces pasaje de término y queda: 4m = 3, haces pasaje de factor como divisor y queda:
m = 3/4, que conduce a la recta cuya ecuación es: y = (3/4)x + 1.
Espero haberte ayudado.
-
Por favor, ayuda con este ejercicio de circunferencia en el plano cartesiano:
El centro de una circunferencia que pasa por (1,-2) y (-2,2) está situado sobre la recta de la ecuación 8x -4y +9 = 0 ¿Cuál es la ecuación?
Antonio Silvio Palmitano
el 17/8/17Puedes designar a las coordenadas del centro de la circunferencia: C(h,k),
y como tienes que pertenece a la recta, reemplazas sus coordenadas en su ecuación y queda:
8h - 4k + 9 = 0 (1).
Luego, plantea la ecuación cartesiana canónica de la circunferencia (observa que designamos al radio con R):
(x - h)2 + (y - k)2 = R2,
luego, como tienes dos puntos que pertenecen a la circunferencia, reemplazas sus coordenadas en su ecuación y quedan dos ecuaciones:
(1 - h)2 + (- 2 - k)2 = R2 (2),
(- 2 - h)2 + (2 - k)2 = R2 (3),
luego, con las ecuaciones señaladas (1) (2) (3) tienes el sistema de tres ecuaciones con tres incógnitas:
8h - 4k + 9 = 0
(1 - h)2 + (- 2 - k)2 = R2
(- 2 - h)2 + (2 - k)2 = R2,
igualas los primeros miembros de las dos últimas ecuaciones y queda;
8h - 4k + 9 = 0
(1 - h)2 + (- 2 - k)2 = (- 2 - h)2 + (2 - k)2,
desarrollas los binomios elevados al cuadrado en la segunda ecuación y el sistema queda:
8h - 4k + 9 = 0
1 - 2h + h2 + 4 + 4k + k2 = 4 + 4h + h2 + 4 - 4k + k2,
haces pasajes de términos en la segunda ecuación, reduces términos semejantes (observa que tienes cancelaciones), y el sistema queda:
8h - 4k + 9 = 0
- 6h + 8k - 3 = 0, aquí haces pasajes de términos y queda: 8k = 6h + 3, divides por 8 en todos los términos y queda: k = (3/4)h + 3/8 (4),
luego sustituyes la expresión señalada (4) en la primera ecuación y queda:
8h - 4( (3/4)h + 3/8 ) + 9 = 0, distribuyes el segundo término y queda:
8h - 3h - 3/2 + 9 = 0, reduces términos semejantes, haces pasaje de término y queda:
5h = - 15/2, haces pasaje de factor como divisor y queda:
h = - 3/2,
luego reemplazas en la ecuación señalada (4) y queda:
k = (3/4)(- 3/2) + 3/8, resuelves el primer término, reduces términos semejantes y queda:
k = - 3/4,
luego, tienes que el centro de la circunferencia tiene coordenadas: C( -3/2 , -3/4 ):
luego reemplazas valores en las ecuaciones señaladas (2) (3) y quedan:
(1 - (-3/2))2 + (- 2 - (-3/4))2 = R2
(- 2 - (-3/2))2 + (2 - (-3/4))2 = R2,
resuelves términos numéricos y quedan:
25/4 + 25/16 = R2
1/4 + 121/16 = R2,
resuelves los primeros miembros, y ambas ecuaciones quedan:
125/16 = R2,
haces pasaje de potencia como raíz y queda:
√(125/16) = R.
Luego, reemplazas valores en la ecuación canónica de la circunferencia, y queda:
( x - (-3/2) )2 + ( y- (-3/4) )2 = ( √(125/16) )2,
resuelves signos en los argumentos de los binomios, simplificas índice y exponente en el segundo miembro y queda:
(x + 3/2)2 + (y + 3/4)2 = 125/16.
Espero haberte ayudado.
-
sea f(x)= √ΙxΙ, x<-1 y ax+b, x≥-1 calcule a y b de modo que sea derivable en x=-1
¿como puedo sacar la derivada de √ΙxΙ ?
Antonius Benedictus
el 16/8/17Antonio Silvio Palmitano
el 16/8/171)
La función debe ser continua en x = -1:
a) f(-1) = a(-1) + b = - a + b (a determinar);
b) Límites laterales:
Lím(x→-1-) f(x) = Lím(x→-1-) √(|x|) = Lím(x→-1-) |-1| = 1,
Lím(x→-1+) f(x) = Lím(x→-1+) (ax + b) = a(-1) + b = - a + b,
luego, como los límites laterales deben ser iguales queda la ecuación:
- a + b = 1 (1),
por lo que tienes:
f(- 1) = 1.
2)
Plantea las derivadas laterales de la función evaluadas para x = - 1:
f-' (-1) = Lim(h→0-) ( f(-1+h) - f(-1) )/h = Lim(h→0-) ( √(|-1+h|) - 1 )/h =
= Lim(h→0-) ( √(|-1+h|) - 1 )/h,
y observa que el argumento del límite es negativo, por lo que aplicas la definición de valor absoluto y queda:
= Lim(h→0-) (√(- (- 1 + h) ) - 1)/h = Lim(h→0-) (√(1 - h) - 1)/h =
racionalizas el numerador y queda:
= Lim(h→0-) (√(1 - h) - 1)(√(1 - h) + 1) / h(√(1 - h) + 1) =
= Lim(h→0-) ( (1 - h) - 1 ) / h(√(1 - h) + 1) =
= Lim(h→0-) (1 - h - 1) / h(√(1 - h) + 1) = Lim(h→0-) (- h) / h(√(1 - h) + 1) =
Lim(h→0-) (- 1) / (√(1 - h) + 1) = - 1/2;
f+' (-1) = Lim(h→0+) ( f(-1+h) - f(-1) )/h =
= Lim(h→0+) ( (a(-1+h) + b) - 1 )/h =
= Lim(h→0+) (- a + ah + b - 1)/h =
aplicas la igualdad señalada (1) para el primer y el tercer término del numerador y queda:
= Lim(h→0+) (1 + ah - 1)/h = Lim(h→0+) (ah)/h = a;
luego, como las derivadas laterales deben ser iguales queda:
a = - 1/2,
luego reemplazas en la ecuación señalada (1) y queda:
- (- 1/2) + b = 1, resuelves signos en el primer término y queda:
1/2 + b = 1, haces pasaje de término y queda:
b = 1/2.
Luego, observa que la expresión de la función queda:
f(x) =
√(- x) si x < - 1 ( recuerda que x es negativo, por lo tanto tienes: √(|x|) = √(-x) )
(-1/2)x + 1/2 si x ≥ - 1.
Luego, observa que la expresión de la función derivada queda:
f ' (x) =
- 1/( 2√(- x) ) si x < - 1
- 1/2 si x = - 1
- 1/2 si x > - 1.
Espero haberte ayudado.
-