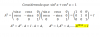-
Vic
el 8/8/17 -
Guillem De La Calle Vicente
el 8/8/17Calcule los puntos de intersección de las parejas de curvas siguientes.
1. 2x2+2y2=5, xy=1
Ángel
el 8/8/17y= √[(5-2x2)/2]
y=1/x
√[(5-2x2)/2] = 1/x
(5-2x2)/2 = 1/x2
x2(5-2x2) = 2
-2x4+5x2-2 = 0
2x4-5x2+2 = 0
2t2-5t+2=0
t=1/2=x2--------> x1= √2/2 , x2= -√2/2
t=2=x2 ----------> x3= √2 , x4= -√2
y1=1/(√2/2) = 2/(√2) = √2
y2=1/(-√2/2) = -2/(√2) = -√2
y3=1/√2 = √2/2
y4=1/-√2 = -√2/2
Puntos de intersección
p1= ( √2/2 , √2 )
p2= ( -√2/2 , -√2 )
p3= ( √2 , √2/2 )
p4= ( -√2 , -√2/2 )
-
lbp_14
el 8/8/17 -
Adrian Chaves Morero
el 8/8/17Hola buenas, podrían decirme como saber si la media es representativa?
Ángel
el 8/8/17Una media es representativa cuando por ejemplo, en tu ejercicio hubiera 4 o 5 valores por encima y 4 o 5 por debajo de la media.
Una media no es representativa cuando hay un número significativo de valores anómalos en proporción al número total de observaciones, como es el caso de tu ejemplo:
*Tienes 10 valores en total y de los cuáles uno excede en mucho a la media (45.0 es el valor anómalo), este hará que la media se desplace hacia la derecha en los números reales y observa que será Media=24.63 (sólo hay dos valores por encima y 8 por debajo)
Entonces la media en tu ejercicio no será representativa por la causa de tener un valor anómalo (el 10%= 1/10 son valores anómalos: un porcentaje muy alto)
-
lbp_14
el 8/8/17 -
Guim
el 8/8/17Ayda porfavor, URGE
Guillem De La Calle Vicente
el 8/8/17
Ángel
el 10/8/17 -
Guillem De La Calle Vicente
el 8/8/17Calcule los puntos de intersección de las parejas de curvas siguientes.
1. x2+y2=25, 3x+4y=0
-
Usuario eliminado
el 8/8/17Hola quería preguntar si está bien echo el ejercicio gracias es el d
-
Victor
el 8/8/17
No encuentro ningun lugar que me explique claramente cómo hacer estos cambios de variable, en vez de explicarlo claramente te ponen un esquemita con simbolos raros como R ( que entiendo que se referirá a racional) y luego pone par o impar, k tras mucho investigar creo que se refiere a las potencias de las funciones seno y coseno. Pues bien, en este ejercicio las potencias son impares y lo resuelve como si fueran pares y ya he flipao por completo. Alguien le encuentra algùn sentido a todo esto??
Antonio Silvio Palmitano
el 8/8/17Observa el argumento de la raíz cuadrada que es denominadora en el argumento de la integral:
senx*cos3x = (senx)1*(cosx)3,
y observa que las suma de los exponentes de los factores es n = 1 + 3 = 4,
y observa que luego de haber sustituido, tienes que puedes simplificar la raíz cuadrada que es denominadora en el denominador del argumento de la integral, por este motivo.
Luego, simplificas expresiones en tu última línea y queda:
... = ∫ ( 1/√(t) )*dt = 2*√(t) + C = 2*√(tanx) + C.
Espero haberte ayudado.
Victor
el 8/8/17 -
José Gómez-Vizcaíno Escudero
el 8/8/17
Cuestión A1, b)? Gracias!!
