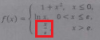¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

Continuidad y limites laterales

Continuidad y limites laterales

Función a trozos - Discontinuidad 01

Función a trozos - Discontinuidad 02

Función a trozos - Discontinuidad 03

Pero hay una región determinada por las cuatro curvas:

y=2x-3x²

3x²-2x+y=0

Utiliza la fórmula para ec. de 2º grado con a=3, b=-2, c=y ; 

obtendrás dos valores de x, sustituyes en esos valores la y por la x y obtendrás la función inversa.

Completamos.

Observa que la función cuya expresión tienes en tu enunciado tiene dominio: D = R = (-∞,+∞).

Aplicas la fórmula resolvente y las soluciones quedan:

x = ( 2 ± √(4 - 12y) )/6 (1),

luego, observa que para que la expresión tenga sentido, debe cumplirse la condición:

4 - 12y ≥ 0, haces pasaje de término y queda:

- 12y ≥ - 4, haces pasaje de factor como divisor (observa que cambia la desigualdad) y queda:

y ≤ 1/3, por lo que tienes que la imagen de la función es: I = (-∞,1/3].

Luego, permutas variables en la ecuación señalada (1) y queda:

y = ( 2 ± √(4 - 12x) )/6, 

que está definida en el dominio: D₁ = (-∞,1/3],

y observa que tienes dos opciones:

a) 

y = ( 2 - √(4 - 12x) )/6,

cuyos valores son menores que (2 - 0)/6 = 1/3, por lo que su imagen es: I₁ = (-∞,1/3],

b)

y = ( 2 + √(4 - 12x) )/6,

cuyos valores son mayores que (2 + 0)/6 = 1/3, por lo que su imagen es: I₂ = [1/3,+∞).

Por lo tanto, puedes concluir que las expresiones de las funciones inversas son las indicadas en los apartados (a) y (b),

con las restricciones que indican sus imágenes, que son las restricciones correspondientes que debes realizar en el dominio de la función.

Espero haberte ayudado.

Se puede simplificar un poco:

a)  y = [2 - √(4 - 12x) ]/6  =     {2 - √[4*(1-3x)] }/ 6  =   [2 - 2√(1-3x) ]/ 6  =  [1-√(1-3x)]/3

b)  y = [2 + √(4 - 12x) ]/6  =     {2 + √[4*(1-3x)] }/ 6   =   [2 + 2√(1-3x) ]/ 6  =  [1+√(1-3x)]/3

P(Número_1) = P(Número_3) = P(Número_5) = 1/9

P(Número_2) = P(Número_4) = P(Número_6) =2/9

Probabilidad(Par)= P(Número_2) + P(Número_4) + P(Número_6) = 2/9 + 2/9 + 2/9 = 6/9 = 2/3

Probabilidad(Primo)= P(Número_2) +  P(Número_3) + P(Número_5) = 2/9 + 1/9 + 1/9 =   4/9

¿Qué pone dentro del recuadro rojo?

Es x/e no le di cuenta que no se veía bien 

f(x) es continua por definición de cada uno de los trozos (polinómica y logarítmica), excepto en x=0 y x=e, que de momento no sabemos y la estudiaremos en particular:

Continuidad en x=0

(lim x->0-) 1+x^2=  1

(lim x->0+) lnx=  -inf

Entonces f(x) en x=0 presenta una discontinuidad de salto infinito en la derecha

Continuidad en x=e

(lim x->e-) lnx=  1

(lim x->e+) x/e=  1

Entonces f(x) en x=e es contínua

Por lo tanto f(x) es contínua en (-inf,0) U (0,inf) = ℛ - {0}

1) 43/52 : (52/43) -1 =   (43/52)  ÷ (43/52) =  k ÷ k =      1

2) ¿Cuántas botellas de 120ml se necesitan para llenar un recipiente de 132 L ?   ((120ml=0.12litros))

1 botella = 0.12 litros

x botellas = 132 litros

x= (1*132)/ 0.12 = 1100 botellas

Muchas gracias por ayudarme!!! :)

3) Si el perímetro de la Tierra es 4.104 y una hormiga mide 5mm. ¿Cuántas hormigas en fila se necesitan para rodear la tierra?

P= 4*104m = 40.000 metros

H= 0.005 metros

0.005x = 40000

x= 40000/0,005

x= 8.000.000 = 8*10⁶

sin4x = sin(90-2x)    //Estoy casi seguro que cuando son RT iguales los ángulos también lo son. Por lo tanto:

4x = 90 - 2x

6x = 90

x = 15

Tienes la ecuación trigonométrica que indica el colega Diego:

sen(4x) = sen(90° - 2x), aplicas la identidad del seno del ángulo complementario en el segundo miembro y queda:

sen(4x) = cos(2x), aplicas la identidad del seno del doble de un ángulo en el primer miembro y queda:

2*sen(2x)*cos(2x) = cos(2x), haces pasaje de término y queda:

2*sen(2x)*cos(2x) - cos(2x) = 0, extraes factor común y queda:

cos(2x)*(2*sen(2x) -1) = 0,

luego, por anulación de un producto, tienes dos opciones:

a)

cos(2x) = 0, compones con la función inversa del coseno y queda:

2x = 90° + 180°*k, divides por 2 en todos los términos de la ecuación y queda:

x = 45° + 90°*k, con k ∈ Z (observa que algunas de estas soluciones son: 45°, 135°, 225°, 315°)

b)

2*sen(2x) - 1 = 0, haces pasaje de término y queda:

2*sen(2x) = 1, haces pasaje de factor como divisor y queda:

sen(2x) = 1/2, compones con la función inversa del seno y quedan dos opciones:

b₁)

2x = 30° + 360°*m (en el primer cuadrante), divides por 2 en todos los términos de la ecuación y queda:

x = 15° + 180°*m, con m ∈ Z (observa que algunas de estas soluciones son: 15°, 195°)

b₂)

2x = 150° + 360°*n (en el segundo cuadrante), divides por 2 en todos los términos de la ecuación y queda:

x = 75° + 180°*n, con n ∈ Z (observa que algunas de estas soluciones son: 75°, 255°).

Espero haberte ayudado.

Hola Antonio!

a)

Para calcular los puntos de corte con los ejes tienes que:

En el eje X → Igualar la y a 0, es decir, tienes que resolver la ecuación de segundo grado x² - 5x + 6 = 0

En el eje Y → Igualar la x a 0, es decir, sustituye en la ecuación x² - 5x + 6 la x por 0

b)

Para calcular la ecuación de la recta dados dos puntos tienes que calcular la ecuación continua de la recta, y luego, si quieres, la pasas a otra forma.

Dados los dos puntos A (x₁, y₁) y B (x₂, y₂).

Calculas el vector director que forman los puntos.

V (v₁, v₂)

v₁ = x₂ - x₁

v₂ = y₂ - y₁

Sustituyes los valores en la ecuación continua y ya está:

(x - x₁) / v₁ = (y - y₁) / v₂

Soluciones:

a)

Puntos de corte con el eje X → x₁ = 3, x₂ = 2

Puntos de corte con el eje Y → y = 6

b)

(x - 1) / -2 = (y - 4) / 2

Espero que lo entiendas.

Saludos.