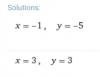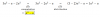-
Una pregunta, cuál sería la derivada de e^(-x) ??
Gracias!
-
Buenos dias ,
necesitaría ayuda con este ejercicio, después de realizar algunos de matrices y ver todo el temario de matrices de unicoos no se por donde empezar a plantear este ejercicio.
Gracias y un saludo.
Antonius Benedictus
el 8/8/17Alejandro Álvarez
el 8/8/17 -
David
el 13/8/17Lo siento pero no entiendo bien el enunciado...
Se trata además de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado, pero no olvidéis de adjuntarlo de forma LITERAL, para saber que os piden. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-) -
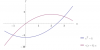
Calcule los puntos de intersección de las parejas de curvas siguientes.
1. y=x2+3, y=3x+1
-
Antonio Silvio Palmitano
el 8/8/17a)
Aplicamos la definición de continuidad de una función en un elemento de su dominio:
1) f(1) = 1/1 - 3 = 1 - 3 = - 2,
2) Límites laterales:
Lím(x→1-) f(x) = Lím(x→1-) (m*x - 1) = m*1 - 1 = m - 1,
Lím(x→1+) f(x) = Lím(x→1+) (1/x - 3) = 1/1 - 3 = 1 - 3 = - 2,
luego, plantea la igualdad entre los límites laterales y queda:
m - 1 = - 2, haces pasaje de término y queda: m = - 1,
3) La función es continua si m = 1, y la expresión de la función queda:
f(x) =
- x - 1 si x < 1
1/x - 3 si x ≥ 1,
y observa que el dominio de la función es el conjunto de los números reales.
b)
Puedes plantear, por definición, las derivadas laterales
f-' (1) = Lím(h→0-) ( f(1+h) - f(1) )/h = Lím(h→0-) (-(1+h)-1 - (-2) )/h =
= Lím(h→0-) (-1-h-1+2)/h = Lím(h→0-) (- h)/h = - 1,
f+' (1) = Lím(h→0+) ( f(1+h) - f(1) )/h = Lím(h→0+) (1/(1+h)-3 - (-2) )/h =
= Lím(h→0+) (1/(1+h) - 1)/h = Lím(h→0+) ( 1 - (1+h) ) / (1+h)h =
= Lím(h→0+) (- h) / (1+h)h = Lím(h→0+) - 1 / (1+h) = - 1,
y como las derivadas laterales son iguales, tienes que la derivada de la función evaluada en x = 1 es igual a -1,
y la expresión de la función derivada queda
f ' (x) =
- 1 si x < 1
- 1 si x = 1
- 1/x2 si x > 1,
y observa que el dominio de la función derivada es el conjunto de los números reales.
Espero haberte ayudado.