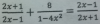-
Antonius Benedictus
el 8/8/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Antonio Silvio Palmitano
el 7/8/17Plantea la condición de punto estacionario, por medio de las derivadas parciales de la función:
fx = 0
fy = 0
fλ = 0,
sustituyes expresiones y queda:
1 - 2λx = 0, de aquí despejas (observa que λ y x deben ser ambos distintos de cero): 1/(2x) = λ (1)
1 - 2λy = 0
- x2 - y2 + 1 = 0,
luego sustituyes la expresión señalada (1) y el sistema queda:
1 - y/x = 0, de aquí despejas: x = y (2)
- x2 - y2 + 1 = 0,
luego sustituyes la expresión señalada (2) en la última ecuación y queda:
- 2y2 + 1 = 0, de aquí despejas: y2 = 1/2 = 2/4, y luego tienes dos opciones:
a)
y = - √(2)/2, sustituyes en las expresiones señaladas (2) (1) y queda: x = - √(2)/2, - √(2)/2 = λ;
b)
y = √(2)/2, sustituyes en las expresiones señaladas (2) (1) y queda: x = √(2)/2, √(2)/2 = λ.
Por lo tanto, tienes que la gráfica de la función presenta dos puntos estacionarios: A(- √(2)/2,- √(2)/2,- √(2)/2) y B(√(2)/2,√(2)/2,√(2)/2).
Espero haberte ayudado.
-
Ángel
el 7/8/17(2x+1)/(2x-1) + 8/(1-4x2) = (2x-1)/(2x+1)
(2x+1)/(2x-1) + 8/-(4x2-1) = (2x-1)/(2x+1)
-[(2x+1)(2x+1)]/-(2x-1)(2x+1) + 8/-(4x2-1) = -[(2x-1)(2x-1)]/-(2x+1)(2x-1)
-[(2x+1)(2x+1)]/-(4x2-1) + 8/-(4x2-1) = -[(2x-1)(2x-1)]/-(4x2-1)
-[(2x+1)(2x+1)] + 8 = -[(2x-1)(2x-1)]
-(4x2+4x+1) + 8 = -(4x2-4x+1)
(-4x2-4x-1) +8 = -4x2+4x-1
-4x+7=4x-1
8x= 8
x= 1
-
Antonio Silvio Palmitano
el 7/8/17Observa que la expresión de la función es un producto, cuyos factores son:
u = (x2+x)/(3x-5), cuya derivada queda: u ' = ( (2x+1)(3x-5) - (x2+x)(3) ) / (3x-5)2.
v = √(2x2-x-6), cuyas derivada queda (observa que debes aplicar la regla de la cadena): v ' = (4x-1) / 2√(2x2-x-6);
luego, evalúa las expresiones para x = 3 y quedan:
u(3) = 12/4 = 3,
u ' (3) = (7*4 - 12*3)/42 = (28 - 36)/16 = - 8/16 = - 1/2,
v(3) = √(18-3-6) = √(9) = 3,
v ' (3) = 11 / 2*3 = 11/6.
Luego, como la expresión de la función es un producto: f(x) = u*v,
tienes que la expresión de su función derivada evaluada queda:
f ' (3) = u ' (3) * v(3) + u(3) * v ' (3) = (- 1/2)*3 + 3*(11/6) = - 3/2 + 11/2 = 8/2 = 4.
Luego, evalúa la expresión de la función y queda:
f(3) = u(3)*v(3) = 3*3 = 9,
y tienes que el punto A(3,9) es el punto de la gráfica de la función que tienes en estudio en este ejercicio.
Luego, plantea la pendiente de la recta tangente:
mT = f ' (3) = 4,
y su ecuación cartesiana queda: y - 9 = 4(x - 3), que en forma explícita queda: y = 4x - 3.
Luego, plantea la pendiente de la recta normal:
mN = -1 / f ' (3) = -1/4,
y su ecuación cartesiana queda: y - 9 = - (1/4)(x - 3), que en forma explícita queda: y = - (1/4)x + 39/4.
Espero haberte ayudado.
-
Ayuda Por favor
Las notas de siete alumnos son 08; 09; 10; 11; 12; 08 y 14. Un alumno aprueba, si su nota es mayor que la media y la mediana. ¿ Cuantos alumnos aprobaron?
Tema: Medidas de Tendencia Central
Ángel
el 7/8/17Notas colocadas en orden: 08; 08; 09; 10; 11; 12; 14 ----------> 10 es la mediana
(08+08+09+10+11+12+14)÷ 7 = 72÷7= 10.29 es la media
4 alumnos < mediana y media < 3 alumnos <--------> 4 alumnos < 10.29 < 3 alumnos
-----------------------------------------------------------------------------------------------------------------------------------------
Conclusión: Aprobaron 3 alumnos con las notas 14,12 y 11 y los otros 4 suspendieron
-
Hola. Tengo una gran duda...Respecto al Método de disco y arandelas.
¿En qué caso podría usarlas cada una?
¿En qué se diferencian?Ejemplo:
*Al usar el Método de las Arandelas me sale diferentes respuestas.
*Por método de los discos(me ayudaron aquí)
Antonius Benedictus
el 8/8/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
se lanzan 5 monedas. halla la probabilidad de:
a). sacar 3 caras.
b). sacar al menos 2 caras.
c). no sacar ninguna cara
Ángel
el 7/8/17Probabilidad= Casos favorables/Casos posibles
x= Cruz
c= Cara
Con 5 monedas hay 25= 32 combinaciones de resultados diferentes = 32 casos posibles
Los casos favorables están resaltados en las listas en "negrita"
a) P(c=3)= Sacar exactamente 3 caras = 10/32
[ {x,x,x,x,x}, {x,x,x,x,c}, {x,x,x,c,x}, {x,x,x,c,c}, {x,x,c,x,x}, {x,x,c,x,c}, {x,x,c,c,x}, {x,x,c,c,c}, {x,c,x,x,x}, {x,c,x,x,c}, {x,c,x,c,x}, {x,c,x,c,c}, {x,c,c,x,x}, {x,c,c,x,c}, {x,c,c,c,x}, {x,c,c,c,c}, {c,x,x,x,x}, {c,x,x,x,c}, {c,x,x,c,x}, {c,x,x,c,c}, {c,x,c,x,x}, {c,x,c,x,c}, {c,x,c,c,x}, {c,x,c,c,c}, {c,c,x,x,x}, {c,c,x,x,c}, {c,c,x,c,x}, {c,c,x,c,c}, {c,c,c,x,x}, {c,c,c,x,c}, {c,c,c,c,x}, {c,c,c,c,c} ]
---------------------------------------------------------------------------------------------------------------------------------------------
b) P(c ≥2)= sacar al menos 2 caras = 1- p(1cara) - p(ninguna cara) = 1 - 5/32 - 1/32= 26/32 = 13/16
[ {x,x,x,x,x}, {x,x,x,x,c}, {x,x,x,c,x}, {x,x,x,c,c}, {x,x,c,x,x}, {x,x,c,x,c}, {x,x,c,c,x}, {x,x,c,c,c}, {x,c,x,x,x}, {x,c,x,x,c}, {x,c,x,c,x}, {x,c,x,c,c}, {x,c,c,x,x}, {x,c,c,x,c}, {x,c,c,c,x}, {x,c,c,c,c}, {c,x,x,x,x}, {c,x,x,x,c}, {c,x,x,c,x}, {c,x,x,c,c}, {c,x,c,x,x}, {c,x,c,x,c}, {c,x,c,c,x}, {c,x,c,c,c}, {c,c,x,x,x}, {c,c,x,x,c}, {c,c,x,c,x}, {c,c,x,c,c}, {c,c,c,x,x}, {c,c,c,x,c}, {c,c,c,c,x}, {c,c,c,c,c} ]
--------------------------------------------------------------------------------------------------------------------------------------------
c) P(c=0)= no sacar ninguna cara = todas cruz = 1/32
[ {x,x,x,x,x}, {x,x,x,x,c}, {x,x,x,c,x}, {x,x,x,c,c}, {x,x,c,x,x}, {x,x,c,x,c}, {x,x,c,c,x}, {x,x,c,c,c}, {x,c,x,x,x}, {x,c,x,x,c}, {x,c,x,c,x}, {x,c,x,c,c}, {x,c,c,x,x}, {x,c,c,x,c}, {x,c,c,c,x}, {x,c,c,c,c}, {c,x,x,x,x}, {c,x,x,x,c}, {c,x,x,c,x}, {c,x,x,c,c}, {c,x,c,x,x}, {c,x,c,x,c}, {c,x,c,c,x}, {c,x,c,c,c}, {c,c,x,x,x}, {c,c,x,x,c}, {c,c,x,c,x}, {c,c,x,c,c}, {c,c,c,x,x}, {c,c,c,x,c}, {c,c,c,c,x}, {c,c,c,c,c} ]
sheyla
el 7/8/17Jordano Tinoco
el 7/8/17En el apartado b lo que te quiere decir es lo siguiente:
Es mas facil sacar la secuencia 0,1 que una suma que vaya desde 2 hasta el infinito, cierto?, entonces, como toda probabilidad vale 1 sacamos la secuencia de 0, 1 se la restamos a 1 para no tener que sacar la probailidad de 2, 3, 4, 5....... n y luego sumarlas. Para ejemplificar mejor, hay una formula en probabilidad que dice, La probabilidad de que suceda un evento, es igual 1 menos que no suceda, porque menos 1, porque la probabilidad vale 1 siempre, se expresa de la siguente manera P(Alguno)= 1-P(ninguno), entonces tenemos el principio basico de laplace que es Casos favorables/Casos posibles, el problema te dice que tienes dos opciones cara o cruz (x=2) y tienes 5 monedas (n=5) la formula para sacar los casos posibles es #(S)=nORx por tanto quedaria así
#=Cardinalidad
#(S)= 5OR2=25=32
#(x)=5 ,{x,x,x,x,c}, {x,x,x,c,x}, {x,x,c,x,x}, {x,c,x,x,x}, {c,x,x,x,x}, hay cinco formas de que den solo una cara#(c)=1 {x,x,x,x,x} hay solo una forma de que no de ninguna cara
P(x ≥2)= 1-P(≤2)
= 1-{Casos favorables/ casos posibles}
=1-(5/32+1/32}
=1-6/32
P(x ≥2)=13/16
Espero haberte aclaro tu duda, es otra forma de hacerlo, pero si te basas en esta pequeña explicacion con el ejemplo de arriba que esta mucho mas completo lo entenderas mejor
Ángel
el 7/8/17Al menos una cara=31/32
[
{x,x,x,x,x}, {x,x,x,x,c}, {x,x,x,c,x}, {x,x,x,c,c}, {x,x,c,x,x}, {x,x,c,x,c}, {x,x,c,c,x}, {x,x,c,c,c}, {x,c,x,x,x}, {x,c,x,x,c}, {x,c,x,c,x}, {x,c,x,c,c}, {x,c,c,x,x}, {x,c,c,x,c}, {x,c,c,c,x}, {x,c,c,c,c}, {c,x,x,x,x}, {c,x,x,x,c}, {c,x,x,c,x}, {c,x,x,c,c}, {c,x,c,x,x}, {c,x,c,x,c}, {c,x,c,c,x}, {c,x,c,c,c}, {c,c,x,x,x}, {c,c,x,x,c}, {c,c,x,c,x}, {c,c,x,c,c}, {c,c,c,x,x}, {c,c,c,x,c}, {c,c,c,c,x}, {c,c,c,c,c} ]Observa que hemos descartado sólo la combinación de todas las cruces.
Al menos dos caras=26/32= 13/16
[
{x,x,x,x,x},{x,x,x,x,c},{x,x,x,c,x},{x,x,x,c,c},{x,x,c,x,x}, {x,x,c,x,c}, {x,x,c,c,x}, {x,x,c,c,c},{x,c,x,x,x}, {x,c,x,x,c}, {x,c,x,c,x}, {x,c,x,c,c}, {x,c,c,x,x}, {x,c,c,x,c}, {x,c,c,c,x}, {x,c,c,c,c},{c,x,x,x,x}, {c,x,x,x,c}, {c,x,x,c,x}, {c,x,x,c,c}, {c,x,c,x,x}, {c,x,c,x,c}, {c,x,c,c,x}, {c,x,c,c,c}, {c,c,x,x,x}, {c,c,x,x,c}, {c,c,x,c,x}, {c,c,x,c,c}, {c,c,c,x,x}, {c,c,c,x,c}, {c,c,c,c,x}, {c,c,c,c,c} ]Hemos descartado la combinación de todas las cruces Y EN LAS QUE HAY UNA SOLA CARA.
-
el numero de aniemales en 1 granja son 9000 entre conejos y gallinas. tienen sobrepeso 4000 animales, que son 35% conejos y 60% gallinas. calcula el numero de conejos y gallinas de la granja.
Ángel
el 7/8/17Incógnitas
Conejos=x
Gallinas=y
Sistema de ecuaciones
(*) x+y=9000
(**) 0.35x+0.6y=4000
Multiplicamos (*) por 7 y multiplicamos (**) por -20
7x +7y= 63000
-7x -12y= -80000
Obtenemos el número de gallinas
-5y= -17000
y= 3400 gallinas
Y el nº de conejos
x+y=9000
x+3400=9000
x= 5600 conejos