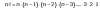-
Hola,me pueden ayudar con este ejercicio por favor : Hallar la suma de los múltiplos de 17 que no son múltiplos de 5 entre 4000 y 12500..desde ya muchas gracias
Ángel
el 24/7/174000:17=235.29...
El primer número que es múltiplo de 17 que no es múltiplo de 5 entre 4000 y 12500 es: 236*17= 4012
Conjunto de múltiplos de 17 entre 4000 y 12500: A= {4012, 4012+17, (4012+17)+17, .....12495}
Los números a descartar del conjunto anterior son: B={4080, 4080+85, (4080+85)+85, ......., 12495} <-----------Múltiplos de 5 del conjunto A
C= A-B
Conjunto buscado: Suma de los elementos de C
-
Guillem De La Calle Vicente
el 24/7/17Ángel
el 24/7/17 -
Ayuda necesito generalizar un factorial en concreto (2n)!, por las definiciones del factorial se que (2n)! = (2n)*(2n-1)...*(2*2)*(2*1), pero como existen n terminos seria mas o menos como esto (a1)*(a2)*...*(an-1)*(abn) = (a^n)b! entonces asumiria que (2n)!=(2^n)n! pero si cualculo con n=3, (2*3)!=(2*3)*(2*2)*(2*1)= (2^3)3! = 48 pero
(2*3)!=6!=720, por lo tanto (2n)! no es igual a (2^n)n!.
Ayudenme mañana tengo examen y necesito saber como reducir ese factorial.
-
Hola, que tal, alguien me podría ayudar con el ejericio Nº11 de analisis matemático 1. No lo entiendo, intente varias veces pero no pude y la solución según el libro es x > 30.000
-
En un colegio el 80% de los colegiales estudian inglés, y de cada tres colegiales, uno estudia inglés y francés.¿ La probabilidad de que un estudiante de inglés lo sea también de francés es?
-
¿Es convergente la sucesión a(k+1) = 3 + (1/3)sen(pi·a(k)/2); a(0)=0? Si es convergente, ¿a partir de qué n dista a(n) del límite menos de 10^(-3)?
Antonius Benedictus
el 24/7/17