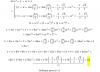-
Antonius Benedictus
el 5/7/17Ylenia Montes
el 5/7/17Antonius Benedictus
el 5/7/17 -
alguien sabe como resolver esta serie Σn=2 a ∞ 1/(n^2-1) ?? el resultado es 3/4.
Guillem De La Calle Vicente
el 5/7/17Separa en fracciones simples (te salen 2 series armonicas), y esas 2 series las puedes "sumar", y por sumar me refiero a poner una equivalencia (usando la Constante de Euler-Mascheroni).
No recuerdo exactamente como era, mira la definición de la constante esa, y cambia las series por logaritmos, a ver si te sale!
Me he colado, aunque se puede hacer lo que te he dicho, en este caso no hace falta (usar la constante).
Descompon en fracciones simples.
Separa en 2 sumas.
Ajusta el índice para que te quede la serie armónica de 1/n (desde algun n, a lo mejor 2, o 3). Y finalmente resta, y te queda -3/4...
(para verlo mas claro, en el paso del indice yo suelo sumar (y restar) los terminos necesarios para que la serie empiece en el mismo indice en ambos casos, e ir mas seguro)
-
 ¿Alguien podría ayudarme con este ejercicio? Calcular las coordenadas que me piden sé hacerlo, pero lo primero no estoy segura si es como pienso. ¡Muchas gracias!
¿Alguien podría ayudarme con este ejercicio? Calcular las coordenadas que me piden sé hacerlo, pero lo primero no estoy segura si es como pienso. ¡Muchas gracias!Guillem De La Calle Vicente
el 5/7/17Ylenia Montes
el 5/7/17Guillem De La Calle Vicente
el 5/7/17Guillem De La Calle Vicente
el 5/7/17Ylenia Montes
el 5/7/17Tengo 2 preguntas que hacerles:
1. Para ser una BASE tiene que cumplir que sean linealmente independientes y sistema generador. ¿Puede ser que sean linealmente independientes y que NO sea un sistema generador? ¿Entonces no sería BASE?
2. Estoy en R4 y tengo 4 ecuaciones. ¿Como calcularía una base de ese subespacio?
Guillem De La Calle Vicente
el 5/7/171. Por lo general, para concluir que un conjunto S={v1,v2,...vn} es una base de un espacio vectorial V, es necesario demostrar que S satisface dos condiciones: que S genera V y es linealmente independiente. Sin embargo, si se sabe que V tiene dimensión de n, entonces el siguiente teorema establece que no es necesario verificar ambas condiciones. Basta comprobar una de las dos.
Teorema: Comprobación de una base en un espacio n-dimensional
Sea V un espacio vectorial de dimensión n.
1. Si S={v1,v2,...,vn} es un conjunto de vectores linealmente independientes en V, entonces S es una base de V.
2. Si S={v1,v2,...,vn} genera a V, entonces S es una base de V.
-
Matrices. Averigua si la siguiente afirmación es cierta o no lo es. Demuestra si es cierta o da un contraejemplo si es falsa.
A+B=A+C → B=C.
-
Antonio
el 5/7/17El enunciado es muy fácil de entender, es un sistema de ecuaciones con tres incógnitas, la primera será el número de monedas tipo A, la segunda las de tipo B y la tercera las de tipo C;
de oro tendremos, por un lado x+2y+7z, y por otro 22
de plata tendremos, por un lado 3x+2y+5z, y por otro 22
de cobre tendremos, por un lado x4x+3y+3z, y por otro 56
Planteamos el sistema:
x+2y+7z=22
3x+2y+5z=22
4x+3y+3z=56
lo resolvemos:
x=-23/5
y=147/5
z=-23/5
La solución es absurda, por lo que se deduce que el problema no tiene solución.
-
Les agradecería infinitamente si me pudiesen ayudar con esta derivación límite de (sen(x))^x cuando x tiende a cero por la izquierda, he tratado con L'Hopital pero al parecer el limite no existe, de antemano muchas gracias.
El Cid
el 5/7/17Antonius Benedictus
el 5/7/17 -
Tengo límite cuando x tiende a infinito De:(lnx+x)/(e^-x+x^2).Duda:es inderterminado inf/inf.Si utilizo el criterio de órdenes de infinitos en el numerador es más fuerte el x y en el denominador es más fuerte el x^2.El límite me quedaría 1/x lo que daría cero.Es correcto? El orden de infinitos me dice que el exponencial tiene más peso que el polinómico pero en este caso no puedo tomar el exponencial como de mayor fuerza pues es a elevado a la MENOS infinito lo que da cero.