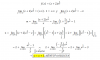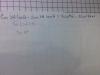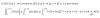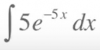-
Hola necesito ayuda con el siguiente problema. Gracias de antemano.
El área de un triangulo es 8 [u ^2 ]. Dos de sus vértices son los puntos A(1, −2) y B(2, 3), y el tercer vértice C pertenece a la recta 2x + y − 2 = 0. Encuentre las coordenadas de C.
Alejandro Legaspe
el 29/6/17Podemos sacarlo con la formula del area de un triangulo, A=bh/2
Digamos que AB es la base, luego, calculemos la norma de AB, sabiendo que AB=(2-1,3-(-2))=(1,5)
|AB|=26½
Luego, podemos saber cuanto vale la altura, pues h=2A/b=2(8)/26½=16/26½Ahora bien, la altura es una distancia que se mide de forma perpendicular desde un vertice hasta una recta, y la distancia de un punto a una recta coincide con eso, pues esta tambien se mide de forma perpendicular desde un punto hasta una recta
Es decir, la altura coincide con la distancia que hay del punto C(a,b) a la recta generada por el vector AB y que pasa por uno de estos dos ultimos puntos, digamos que pasa por A
Encontremos la expresion de la recta que pasa por A y tiene como vector director al AB
(x-1)/1=(y+2)/55x-5=y+2
5x-y-7=0
Ahora, calculemos la distancia del punto C(a,b) a dicha recta, esta distancia coincide con la altura h encontrada16/26½=|5a-b-7|/(26)½
16=|5a-b-7|
Lo anterior ocurre en dos casos, a saber,
Caso 1
5a-b-7=16
Con esta expresion y como C(a,b) pertenece a la recta 2x+y-2=0, cumple esta expresion, es decir 2a+b-2=0, luego con estas dos expresiones se puede plantear el sistema de ecuaciones y resolverlo para encontrar a y b, luego C tiene coordenadas (a,b)Caso 2
-(5a-b-7)=16
Esto es-5a+b+7=16
Analogamente, como C(a,b) pertenece a la recta 2x+y-2=0 se sigue que 2a+b-2=0, con esta y la expresion -5a+b+7=16 se puede encontrar a y b resolviendo el sistema
luego C tiene coordenadas (a,b)
Intentalo y si no sale nos cuentas
-
Nico
el 29/6/17n=1 --> 1²-1= 0 que es divisible por 2
n=2--> 2²-2=2 que es divisible por 2
paso base: supongamos que se cumple para n=k , entonces k²-k es divisble por 2
paso inductivo: probemos que es divisible para el numero siguiente.. n=k+1, entonces:
n= (k+1)²- (k+1)= k²+2k+1-k-1= k²-k que por hipótesis es divisible por 2 .
Saludos!
DueFreitas
el 29/6/17 -
Alejandro Legaspe
el 29/6/17Como bien ya pusiste, la parte de la izquierda es cos(4a), ahora consideremos que cos(4a)=cos(2a+2a)=cos²(2a)-sen²(2a)
Ahora, sabemos que cos2a=cos²a-sen²a y ademas sen2a=2sen(a)cos(a), luegocos(4a)=(cos²a-sen²a)² -(2sen(a)cos(a))²
cos(4a)=cos∧4(a)+sen∧4(a)-2sen²(a)cos²(a)-4sen²(a)cos²(a)=cos∧4(a)+sen∧4(a)-6sen²(a)cos²(a)
Sabemos tambien que sen²a=1-cos²a, luego
cos(4a)=cos∧4(a)+(1-cos²a)²-6cos²(a)(1-cos²a)cos(4a)=cos∧4(a)+1+cos∧4(a)-2cos²a-6cos²a+6cos∧4(a)
cos(4a)=8cos∧4(a)-8cos²a+1Ahi nos cuentas si hay mas dudas
Michelle
el 30/6/17Graciasss!! Entendí todo perfecto 👌🏻. Si te cuento como lo estaba resolviendo me profesora no me creerías. Al principio lo había empezado a resolver como tú, pero no estaba segura, luego lo empezó a resolver la profesora en clases y ahí fue que me enrede y al final ni a ella le salía 🙄. Ojalá tuviera profes como el prof David 😢. En fin muchísimas gracias. Me has salvado la vida 💜.
Alejandro Legaspe
el 30/6/17 -
Buenas noches, tengo una duda, cuando me piden que halle las rectas de regresión de y sobre x , y de x sobre y, hay alguna forma de corroborar que las rectas estén bien?
-
Hola Unicoos, no sé si este problema lo debo plantear con ecuaciones o inecuaciones, me podrian decir los fallos?,
Muchísimas gracias.
El número de visitantes a cierta exposición durante el mes de febrero se incrementó en un 12% respecto al mes de enero. Sin embargo, en marzo sufrió un descenso del 12% respecto a febrero. Si el número de visitantes de enero superó en 36 personas al de marzo, ¿cuántas personas vieron la exposición en enero?
-
Buenas noches. Me podéis explicar esta integral detalladamente es que estoy empezando con las integrales. Gracias.
Pablo
el 28/6/17David
el 28/6/17