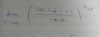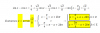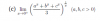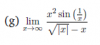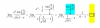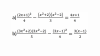-
Mayra
el 29/5/17Hola, alguien podría ayudarme con el inciso a del ejercicio? No se si lo estuve resolviendo bien, pero no se me ocurre forma de salvar la indeterminación para hallar a.
-
Patri Lopez
el 29/5/17Hola!!podeis encontrarme el fallo??? Un saludo y muchas gracias!!
-
Dali
el 29/5/17Hola! Tengo una duda... Este es el enunciado:
"Hallar la ecuación del plano que es paralelo al vector v(2:1:-1) e intercepta a los ejes coordenados OX y OY en a=3 y b=-2 "
Mi duda es, si yo tengo un vector paralelo y el vector que se forma de los puntos a(3:0) y b(0:-2) y Hall in producto vectorial, debería tener el vector perpendicular a ambos y ese sería el vector direccional del plano, pero el problema es que, un vector estaría en 3 dimensiones y el otro solo en dos.. Puedo yo solo poner z=0 y hacer el producto vectorial???
También, el vector que saldría de ese producto vectorial estaria en 2D y para que sea un plano debe tener las tres dimensiones (x,y,z) y no se.. estoy confundida
Neofito 007
el 29/5/17Estas trabajando en 3 dimensiones , los puntos deben estar con 3 componentes
Un punto sobre el eje x tiene por coordenadas
( x , 0 , 0 )
Un punto sobre el eje Y tiene por coordenadas
( 0 , y , 0 )
Un punto sobre el eje z tiene por coordenadas
( 0 , 0 , z )
Con ello creo que puedes tener más claro la situación .
-
IsaacSC
el 29/5/17 -
Angel Garcia Curela
el 29/5/17Disculpe las molestias, pero me encontré con unos ejercicios que no puedo realizar (y no me permiten derivarlos) ¿Me podrían dar una mano?
Daniel Wenli
el 30/5/17
Angel Garcia Curela
el 30/5/17 -
Carlos José Guillén Colón
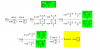
el 29/5/17Buenas Tardes Unicos, quisiera que me ayudaran a resolver estos ejercicios de limites, sin derivar, intente en el de seno con seno suma, y angulo doble, pero no se como resolverlo ya que no se el valor de, y el de logaritmo Natural de x, no se como separarlo del coseno
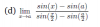
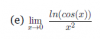
Carlos José Guillén Colón
el 29/5/17
Antonius Benedictus
el 29/5/17 -
Alba Vargas Lozano
el 29/5/17
Ángel
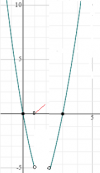
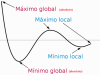
el 29/5/17Los puntos para f(x) el intervalo x∈(-inf,1) se obtienen del trozo: x2-6x
Los puntos para f(x) el intervalo x∈(1,2) se obtienen del trozo: x-1
Los puntos para f(x) el intervalo x∈(2,inf) se obtienen del trozo: x2-9
Sólo tienes que dar valores a la x en la función pertinente (el trozo adecuado) y obtienes un esbozo al menos de la gráfica.
Francisco
el 29/5/17https://www.youtube.com/watch?v=3AP6OodY1W8
Mira este vídeo a partir del minuto 15:45 y ya verás como te ayuda
Ángel
el 29/5/17Te paso unas cuantas coordenadas:
Primer trozo
f(-3)= 27 --------> (-3,27) = (x,y)
f(-2)= 16 --------> (-2,16) = (x,y)
f(-1)= 7 --------> (-1,7)
f(0)= 0 --------> (0,0)
f(0.99999)= -5(+)----> ( 1(-), -5(+) )
Segundo trozo
f(1.00001)= 0(+)
f(1.99999)=1(-)
Tercer trozo
f(2.00001)=-5(+)
f(3)= 0 ------------------> (3,0)
f(4)= 7
.
.
Queda que representes los puntos generados por las coordenadas y los unas en el plano.
-
Isaac
el 29/5/17
-
Fernando
el 29/5/17Ayuda con este ejercicio por favor. He visto todos los vídeos relacionados con el tema, pero no entiendo nada. Se trata de resolver las ecuaciones.
Fernando
el 30/5/17 -
Yessenia Montes Villegas
el 29/5/17
