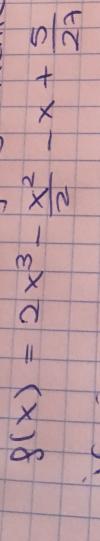-
-
Ángel
el 29/5/17¿De qué curso es?
h(x) = 2x^3 - x^2 + 2x -2
Veamos el signo en x=0:
h(0)= 2*0^3 - 0^2 + 2*0 -2 = -2<0
h(1)= 2x^3 - x^2 + 2x -2 = 1>0
Por lo tanto, aseguramos que se cortan en algún punto situado entre 0 y 1 ----------> h(0,_ _ _ ) = 0
((si quieres averiguar el punto más o menos exacto y eres de Universidad: Newton-Raphson))
-
Hola tengo una pequeña pregunta:
Tengo este siguiente determinante que su resultado da 4
x
y
z
1
1
1
0
2
4y tengo calcularlo sin desarrollar el determinante osea usar las propiedades para sacar el resultado de este otro determinante:
x
y
z
1
1
1
0
1
2El problema que tengo es que no se como incrementar la fila del 0 1 2 al 0 2 4
Tengo la respuesta pero no entiendo bien la razon por la que usa una fracción 1/2 multiplicando esta matriz.
Espero su respuesta.
Gracias por su ayuda.
-
- 1·1=x-3 · ( 2x+9/x2 +9x )
Como se resolvería esto paso a paso porfavor
Ángel
el 29/5/17Juan David Rodríguez González
el 29/5/17Ángel
el 29/5/17Ángel
el 29/5/17Juan David Rodríguez González
el 29/5/17Ángel
el 29/5/17Juan David Rodríguez González
el 29/5/17Juan David Rodríguez González
el 29/5/17Ángel
el 29/5/17No sé si entiendo muy bien tu pregunta....
Teníamos:
2x2-x2+9x-9x-6x-27 = 0 ----------> x2-6x-27=0 ----> x1=9 , x2= -3
Si tuviéramos:
3x2-x2+9x-9x-6x-27 = 0 ------------> 2x2-6x-27=0 ------> x1 y x2 tendrían obviamente un valor distinto al anterior
El "planteamiento" (manera de proceder diría yo), es el mismo.
-
-
Calcula la superficie del recinto limitado por la parábola de ecuación f(x)= x^2 con las rectas de ecuaciones y=x e y=2x
ya lo hice de varias formas pero no me sale de ninguna forma
Me podréis ayudar porfavor
-
Demuestra que, si 1+2+...+n=(1/2)[n+(1/2)]² para n=k≥1, entonces también es ciero para n=k+1. Puedes deducir que la igualdad 1+2+...+n=(1/2)[n+(1/2)]² es válida para todo n∈ℕ.




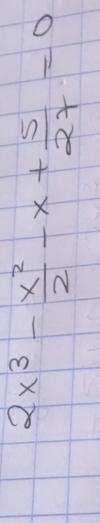

















 Es de este problema
Es de este problema