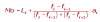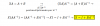Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Camila
el 27/5/17

Hola,necesito ayuda con el siguiente ejercicio:
Una empresa construye pequeños recipientes de base rectangular sin tapa con capacidad de 12cm³. En la base,la longitud de uno de los lados es cinco veces la longitud del otro.Si el costo del material de la base es de $10 por cm² y de $6 para el material de los costados.¿De qué medidas deben construirse los recipientes para gastar lo menos posible?
El tema con el que debe resolverse es derivada,máximos y mínimos.
Gracias!

••0 voto/s
•
Antonius Benedictus
el 27/5/17

•1 voto/s
•
Camila
el 27/5/17
¡ Muchas gracias !

•0 voto/s
•

Cancelar
Joaquin Aguirre
el 27/5/17

Hola necesito ayuda con este ejercicio me cuesta porque no entiendo el pasaje de la forma general a la parametrica

••0 voto/s
•
Neofito 007
el 27/5/17
Llamas a una variable t y resuelves el sistema de ecuaciones para las otras 2 , generalmente se pone z=t , pero puedes y se resuelve para x e y , pero como digo elige el que gustes

•1 voto/s
•
Antonius Benedictus
el 27/5/17

•1 voto/s
•

Cancelar
lbp_14
el 27/5/17

Hola Unicoos,
En este ejercicio me he atascado en calcular la posición de la función respecto la asíntota Horizontal, es decir, poner gráficamente las flechitas en los extremos de los infinitos, y mi profesora dice que se calcula como os he puesto en el papel f(grande)=f(x)-A.Horizontal, etc... y no comprendo eso porque en clase no nos habian salido Asíntotas horizontales hasta ahora y nose como se hace.
Me podrian echar una mano?
Muchisimas gracias

••0 voto/s
•
Neofito 007
el 27/5/17
No entiendo bien tu pregunta con eso de flechitas y de la forma como se pone .
La asintota horizontal de una función (si la tiene ) se calcula tomando límite a (+ infinito) y a (-infinito) Supongo que a algo por allí se refiere con x muy chiquito (muy negativo osea menos infinito) o x muy grande (+ infinito)

Pero tienes un ejemplo resuelto por tu profesora ??

•0 voto/s
•
lbp_14
el 27/5/17
Hola. A lo de las flechas me refiero a dibujar la posición de la función respecto a la asíntota horizontal en sus extremos graficamente. Nosotros solo calculamos la asíntota horizontal con +∞

•0 voto/s
•

Cancelar
Victor
el 27/5/17

Buenas tardes.

Estoy con un ejercicio de PAU 2012 CYL, en concreto este:
Estoy viendo una resolución del ejercicio y he entendido el procedimiento y una de las formas de resolución. Lo que se ha hecho ha sido hallar la derivada de la función en los puntos, y hacer que el producto de pendientes valga -1.

Lo que no he llegado a comprender...es que se utiliza y se pone de ejemplo otro método para llegar a lo mismo.

Dice que se basa en la perpendicularidad en el plano, al cambiar de lado y uno de signo encuentra la perpendicular. En geometría analítica lo entiendo con vectores, aquí soy incapaz de ver de dónde lo está sacando.

••0 voto/s
•
Neofito 007
el 27/5/17
No comprendo muy bien que cosa no tienes claro porque veo que en efecto entiendes de forma clara la solución .

Ahora el decir que el producto de pendientes de 2 rectas perpendiculares es (-1) se expresa como
(m1)(m2) = -1

Otra forma de expresar lo mismo es que pases a uno a dividir
m1 = -1/m2

Es lo mismo , no sé si es tu duda

•0 voto/s
•
Victor
el 27/5/17
Me refiero concretamente a esto:
https://www.youtube.com/watch?v=CPia1gtpVSY&index=10&list=PLunRFUHsCA1zTw6Gxnr651Z6xJJ1cac3g
Minuto 3:37. Dice que hay dos formas de hacerlo, una que no entiendo nada, y la otra que es por producto de pendientes =-1.
Le da el mismo resultado con una que con otra pues es lo mismo, pero no entiendo el planteamiento que da por mucho que le de vueltas.

•0 voto/s
•
Neofito 007
el 27/5/17
No veo vídeos , es mejor que en un texto aclares tu duda , por curiosidad si lo vi esta vez y es justo lo que te acabo de indicar , está expresando lo mismo pero de formas diferentes como allí te indico , en verdad es una sola expresión de otra forma

•0 voto/s
•

Cancelar
Fede E. Guerrero
el 27/5/17

hola tengo una duda, en el video de unicoos https://www.youtube.com/watch?v=ISbnLcFFrNY es correcta la formula de la moda??

••0 voto/s
•
Ángel
el 27/5/17
Sí, es correcta.
La fórmula que utiliza David proporciona un valor aproximado,
y esta: un valor más exacto

•0 voto/s
•
Fede E. Guerrero
el 27/5/17
muchas gracias!

•0 voto/s
•

Cancelar
Miguel
el 27/5/17

Buenas tardes, tengo esta ecuación matricial: AX=A+B. Sé que el próximo paso sería A^-1 × A × X= A^-1 (A+B), pero en caso de que la ecuación fuera XA= A+B como quedaría el próximo paso?
Muchas gracias!

••0 voto/s
•
Antonius Benedictus
el 27/5/17

•1 voto/s
•

Cancelar
Pilar Arias
el 27/5/17

Buenas tardes, ¿Cuál sería el suceso de intersección de a) Extraer una bola coloreada de una urna y extraer un bola roja b)Obtener suma mayor que 6 al lanzar dos dados y obtener número primo en los dos dados
Muchas gracias!

••0 voto/s
•
Antonius Benedictus
el 27/5/17
a) Como se supone que las bolas rojas están coloreadas, la intersección es "extraer bola roja"
b) Obtener una suma mayor que 6 a partir de dos números primos: (2,5),(5,2),(3,5),(5,3),(5,5)

•0 voto/s
•
Ángel
el 27/5/17
Casos posibles: 36 casos
(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)
(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)
(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)
(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)
(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)
(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)

Casos favorables suma mayor que 6:
(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)
(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)
(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)
(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)
(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)
(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)

(Casos favorables suma mayor que 6) y (dos números primos) : 5 casos favorables * Recuerda que el 1 no es primo
(1,6)
(2,5)(2,6)
(3,4)(3,5)(3,6)
(4,3)(4,4)(4,5)(4,6)
(5,2)(5,3)(5,4)(5,5)(5,6)
(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)

Laplace----> Probabilidad(Obtener suma mayor que 6 al lanzar dos dados y obtener dos números primos en los dos dados)=
(5 casos favorables)/(36 casos posibles)= 0.138888= 13.888%

•1 voto/s
•

Cancelar
Cristina Iglesias
el 27/5/17

••0 voto/s
•
Antonius Benedictus
el 27/5/17

•0 voto/s
•

Cancelar
Cristina Iglesias
el 27/5/17

(function(){var g=this;function h(b,d){var a=b.split("."),c=g;a[0]in c||!c.execScript||c.execScript("var "+a[0]);for(var e;a.length&&(e=a.shift());)a.length||void 0===d?c[e]?c=c[e]:c=c[e]={}:c[e]=d};function l(b){var d=b.length;if(0=d.offsetWidth&&0>=d.offsetHeight)a=!1;else{c=d.getBoundingClientRect();var f=document.body;a=c.top+("pageYOffset"in window?window.pageYOffset:(document.documentElement||f.parentNode||f).scrollTop);c=c.left+("pageXOffset"in window?window.pageXOffset:(document.documentElement||f.parentNode||f).scrollLeft);f=a.toString()+","+c;b.b.hasOwnProperty(f)?a=!1:(b.b[f]=!0,a=a<=b.g.height&&c<=b.g.width)}a&&(b.a.push(e),b.c[e]=!0)}p.prototype.checkImageForCriticality=function(b){b.getBoundingClientRect&&q(this,b)};h("pagespeed.CriticalImages.checkImageForCriticality",function(b){n.checkImageForCriticality(b)});h("pagespeed.CriticalImages.checkCriticalImages",function(){r(n)});function r(b){b.b={};for(var d=["IMG","INPUT"],a=[],c=0;c
••0 voto/s
•
Ángel
el 27/5/17
Este código fuente me recuerda al de la fiesta nacional Argentina:

jajajja

•1 voto/s
•

Cancelar