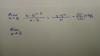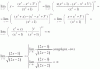-
Buenas, alguien me puede ayudar a continuar? Ya he visto los vídeos de límites pero para este ejemplo no me sirve ..no se como hacerlo
-
Antonio Silvio Palmitano
el 27/5/17Recuerda: si λ es valor propio da A, entonces A*X = λ*X, donde X es un vector propio de A.
a)
Tienes que λ es valor propio da A, entonces:
A*X = λ*X, multiplicas por izquierda por la matriz inversa de A y queda:
A-1*(A*X) = A-1*(λ*X), aplicas la propiedad asociativa del producto en el primer miembro, extraes el factor escalaren el segundo miembro y queda:
(A-1*A)*X = λ*(A-1*X), resuelves el primer factor del primer miembro y queda:
I*X = λ*(A-1*X), aplicas la propiedad del elemento neutro del producto en el primer miembro y queda:
X = λ*(A-1*X), multiplicas en ambos miembros por 1/λ (observa que λ debe ser distinto de cero) y queda:
(1/λ)*X = A-1*X, por lo que tienes que 1/λ es valor propio de A-1.
b)
Tienes que λ es valor propio da A, entonces:
A*X = λ*X, multiplicas por izquierda por la matriz A y queda:
A*(A*X) = A*(λ*X), aplicas la propiedad asociativa del producto en el primer miembro, extraes el factor escalaren el segundo miembro y queda:
A2*X = λ*(A*X), sustituyes el factor remarcado por su expresión en función del valor propio y queda:
A2*X = λ*(λ*X), aplicas la propiedad seudoasociativa del producto de escalar por matriz y queda:
A2*X = λ2*X, por lo que tienes que λ2 es valor propio de A2.
Luego, multiplicas por izquierda por la matriz A y queda:
A*(A2*X) = A*(λ2*X), aplicas la propiedad asociativa del producto en el primer miembro, extraes el factor escalaren el segundo miembro y queda:
A3*X = λ2*(A*X), sustituyes el factor remarcado por su expresión en función del valor propio y queda:
A3*X = λ2*(λ*X), aplicas la propiedad seudoasociativa del producto de escalar por matriz y queda:
A3*X = λ3*X, por lo que tienes que λ3 es valor propio de A3.
Luego, reiteras el procedimiento y tienes que λn es valor propio de An, con n ∈ N.
c)
Recuerda que el determinante de una matriz triangular, en este caso superior, es igual al producto de los elementos de su diagonal principal.
Luego, plantea:
A*X = λ*X, aplicas la propiedad del elemento neutro del producto en el segundo miembro y queda:
A*X = λ*I*X, haces pasaje de término y queda (indicamos con O al vector nulo):
A*X - λ*I*X = O, extraes factor común por derecha y queda:
(A - λ*I)*X = 0, luego, planteas la ecuación característica (observa que la matriz (A - λ*I) también es triangular superior) y tienes:
| A - λ*I | = 0, luego tienes que el primer miembro es igual al producto de los elementos de su diagonal, y queda:
(1 - λ)*(-1 - λ)*(-2 - λ)*(2 - λ) = 0, luego, por anulación de un producto tienes cuatro opciones:
1) 1 - λ = 0, haces pasaje de término y queda: 1 = λ1,
2) -1 - λ = 0, haces pasaje de término y queda: -1 = λ2
3) -2 - λ = 0, haces pasaje de término y queda: -2 = λ3,
4) 2 - λ = 0, haces pasaje de término y queda: 2 = λ4,
Luego, los valores propios de la matriz A9 son:
μ1 = λ19 = 19 = 1,
μ2 = λ29 = (-1)9 = -1,
μ3 = λ39 = (-2)9 = -512,
μ4 = λ49 = 29 = 512.
Espero haberte ayudado.
-
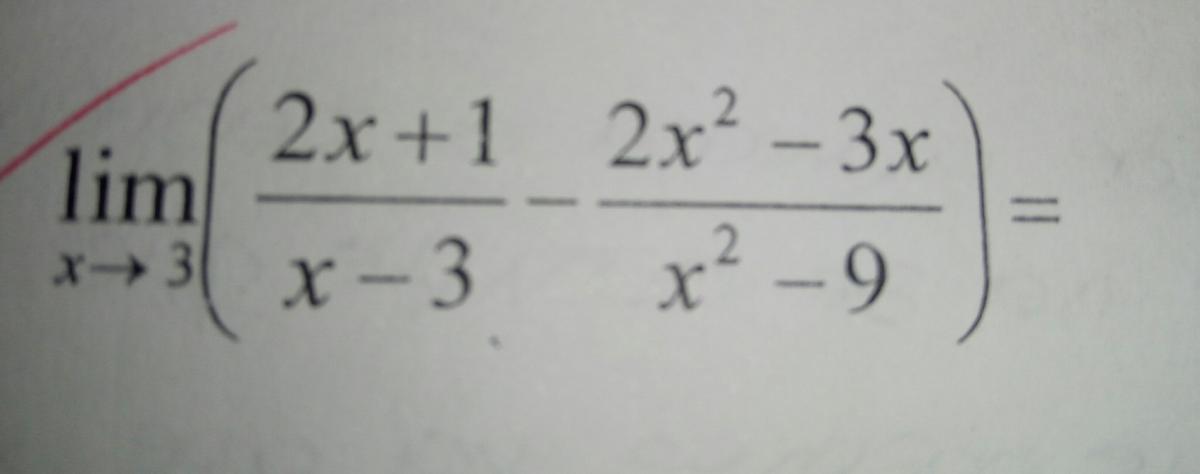 Alguien me puede ayudar a continuar el límite? He llegado a infinito menos infinito que es una indeterminación pero no sé qué hacer ahora , Gracias!
Alguien me puede ayudar a continuar el límite? He llegado a infinito menos infinito que es una indeterminación pero no sé qué hacer ahora , Gracias! -
Usuario eliminado
el 27/5/17I (x) = Q X P
I(X)= (165-x) X (45+x)
I (X) = -X2 +120x + 7425
derivada = -2x+120
60 es un máximo, calculo la imagen de 60 en la función I (X) y sale 11025 euros.
Para el apartado B cojo el apartado precio (45+x)
Sustituyo (45+60) = 105 Respuesta: De 45 a 105 euros
Pero la solución correcta es que el precio debe estar entre 0 y
210 euros
-
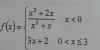
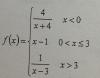 Hola. A ver si pueden ayudarme con estos dos ejercicios de funciones a trozos estudio de la continuidad. A mi el primero me da que es discontinua de salto finito en X igual a cero Y discontinua de salto infinito en X igual a tres. El segundo ejercicio me da que es discontinuidad evitable en X igual a cero y continua en X igual a tres. Los resultados que me da no coinciden con los que me da el ejercicio, Con lo cual no sé si lo tengo bien. Gracias antemano
Hola. A ver si pueden ayudarme con estos dos ejercicios de funciones a trozos estudio de la continuidad. A mi el primero me da que es discontinua de salto finito en X igual a cero Y discontinua de salto infinito en X igual a tres. El segundo ejercicio me da que es discontinuidad evitable en X igual a cero y continua en X igual a tres. Los resultados que me da no coinciden con los que me da el ejercicio, Con lo cual no sé si lo tengo bien. Gracias antemano