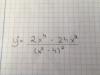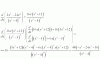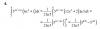Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Alberto Llobregat
el 23/5/17

Necesito ayuda con este problema: muchas gracias

••0 voto/s
•
Antonius Benedictus
el 23/5/17

•1 voto/s
•
Alberto Llobregat
el 23/5/17
Antonio lo entiendo todo menos el I al cuadrado dentro del paréntesis del factor común

•0 voto/s
•
Antonius Benedictus
el 23/5/17
Es la matriz identidad (la equivalente al número 1).
Fíjate, si fuera una cuenta normal:
XA+X=XA+X·1=X(A+1)
En matrices, se pone la matriz identidad (en este caso, de orden 2).

•1 voto/s
•
Antonius Benedictus
el 23/5/17
No es I al cuadrado, sino I sub 2 (identidad, pero de orden 2).

•1 voto/s
•

Cancelar
Ana M Milan
el 23/5/17

No entiendo lo que significa alternativa de contraste e hipótesis nula

••0 voto/s
•
Ana M Milan
el 23/5/17
mañana tengo la selectividad de matemáticas de CS y he encontrado ese ejercicio en un examen de selectividad del 2000. Entonces mañana no me podría salir una pregunta así no?

•0 voto/s
•
Antonius Benedictus
el 23/5/17
Ana, esto es difícil y ya lo han quitado en la nueva Selectividad (al menos en Galicia). Necesitaría un par de horas frente a frente para que te hicieras una idea sobre de qué va el asunto.

•0 voto/s
•
Antonius Benedictus
el 23/5/17
Confirmado: no entra en ningún distrito universitario. En las PAU-LOGSE sí entraba.

•0 voto/s
•

Cancelar
margappavia
el 23/5/17

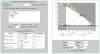
Un distribuidor de aceite acude a una almazara para comprar dos tipos de aceite, A y B. La cantidad máxima que puede comprar es de 12.000 litros en total. El aceite de tipo A cuesta 3 euros/litro y el de tipo B cuesta 2 euros/litro. Necesita adquirir al menos 2.000 litros de cada tipo de aceite. Por otra parte, el coste total por compra de aceite no debe ser superior a 30.000 euros. El beneficio que se conseguirá con la venta del aceite será de un 25 % sobre el precio que ha pagado por el aceite de tipo A y de un 30 % sobre el precio que ha pagado por el aceite de tipo B. ¿Cuántos litros de cada tipo de aceite se deberían adquirir para maximizar el beneficio? Obténgase el valor del beneficio máximo.
No encuentro la función objetivo¿ Como se haría el problema? Gracias

••0 voto/s
•
Antonius Benedictus
el 23/5/17
F(x,y)=3*(0.25)x + 2*(0.30)y

•0 voto/s
•

Cancelar
lbp_14
el 23/5/17

Hola Unicoos
Me pueden ayudar paso a paso con este ejercicio?
Me he quedado atascada
Muchísimas gracias.

••0 voto/s
•
Neofito 007
el 23/5/17
Cada trozo allí mostrado es continuo entonces hay que buscar que los puntos donde cambia de regla de correspondencia sea también continua.

Una de las condiciones para la continuidad es que los límites laterales sean iguales (y sean finitos)
Para este ejercicio con esta condición es suficiente aunque es bueno comprobar las otras condiciones

Continuidad en x= -2
los límites laterales deben ser iguales
Limit x--> -2^- f(x)= 3(-2)+b = -6+b
Limit x--> -2⁺ f(x)= 4
Igualando
-6+b = 4 , entonces b = 10

Continuidad en x = 3
Limit x-->3^- f(x)= 4
Limit x-->3⁺ f(x)= 3a - 2
Igualando
4 = 3a - 2 , entonces a = 2

•1 voto/s
•

Cancelar
Luis Viñedo
el 23/5/17

Lim (x^2 - 3)^x
x→+∞
No entiendo por qué el resultado es infinito.

••0 voto/s
•
Antonius Benedictus
el 23/5/17
No es una indeterminación 1^(+inf), por lo que aquí no se puede aplicar lo del nº e.
La base va a +inf. y el exponente también.
La potencia, entonces, corre a +inf. como alma que lleva el diablo.

•2 voto/s
•

Cancelar
Alejandra Martínez Parra
el 23/5/17

¿Podría alguien ayudarme a realizar la segunda derivada de esta función? No consigo obtener un resultado. Muchas gracias!

••0 voto/s
•
César
el 23/5/17

•0 voto/s
•

Cancelar
Usuario eliminado
el 23/5/17

En el sistema x+y-z = -2
0x -2y + 3z = 8
0x +6y -9z= -4
Me sale SCI y la tengo que parametrizar. Pongo el parametro =z (k)
La duda la tengo en la y, me sale que y= (8-3k) : (-2). Es correcta la Y?

••0 voto/s
•
César
el 23/5/17

•0 voto/s
•

Cancelar
Lili
el 23/5/17

••0 voto/s
•
Antonius Benedictus
el 23/5/17
Ecuaciones de rectas y planos
•0 voto/s
•

Cancelar
Sarah
el 23/5/17

Hola , ¿
podrían ayudarme con este ejercicio de distribución normal porfavor? Copié la corrección de clase y la parte B , no se hacerla por mi sola. Gracias!!¡

••0 voto/s
•
Antonius Benedictus
el 23/5/17
Tal como está formulado el problema, el segundo apartado está mal resuelto. Sale el doble, pues es la probabilidad de que el 1º sí y el 2º no, más la de que el 1º no y el 2º sí.

•0 voto/s
•

Cancelar
Luìs Lòpez
el 23/5/17

Alguien podría Integrar: 5^(4x^3+2x) . (6x^2+1) dx
PD: paso a paso por favor.
Muchas GraciasS!!

••0 voto/s
•
Neofito 007
el 23/5/17
Es inmediato basta hacer
u = 4x³ + 2x
du = (12x² + 2)dx
du = 2(6x² + 1)dx
du/2 = (6x² + 1)dx

Así tienes una integral inmediata

•0 voto/s
•
Luìs Lòpez
el 23/5/17
Hola,
Pero lo que integras es la potencia, pero y el número "5 ^....."
Este es el resultado (No se de donde obtiene el ln)

•0 voto/s
•
Neofito 007
el 23/5/17
Hola por acá me es difícil escribir fórmulas más complicadas como símbolos de integral etc .

Eso lo hace por tabla es decir ya es una fórmula conocida , la integral de a^x dx es (a^x)/(Lna) , eso revisa en tus tablas

•0 voto/s
•

Cancelar