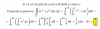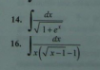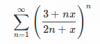-
Júlia Caballol Sangrà
el 10/5/17 -
Mariana Ibañez
el 10/5/17 -
lbp_14
el 10/5/17Hola Unicoos, me dicen si tengo algún fallo en estos dominios, en la segunda no sé cómo justificar que es todo R y en la tercera no sé cómo expresarlo, me lo podrían justificar? Se lo agradecería mucho.
Muchísimas gracias
Neofito 007
el 10/5/17Lo mismo que ya sabes, en la Segunda la única restricción es que el denominador no sea cero, tienes que resolver la ecuación, bueno es cero solo para x=2 Entonces
Dom = R - { 2 }
En el tercero es la misma situación que el segundo caso, el seno es cero en todos los enteros de pi , que se representan como x=k*pi , siendo k un entero
Dom = R - { k*pi } , k es un entero
gonzalezlbl
el 10/5/17- Una aclaratoria: La función es f, y cada elemento del Rango es f(x). Así, que el dominio es de f, no de f(x).
- Del primer ejercicio, el dominio es correcto. Entonces, se debe escribir Domf =ℛ
- 2do ejercicio: No está correcto el dominio dado.
- El dominio es: Domf = {x∈ℛ| 2x- 4 ≠ 0} En palabras sencillas: el denominador NO debe ser cero. Entonces buscamos el valor de x que hace cero al denominador, y lo sacamos del conjunto de los reales:
- 2x- 4 = 0 ⇒ 2x= 4 ⇒ 2x= 22 ⇔ x = 2
- Así, el dominio es: Domf = ℛ - {2}
- El dominio del 3er ejercicio se calcula igual que en el 2do:
- Domf = {x∈ℛ| sen(x)≠0}
- Igual al segundo, calculamos los valores de x que hacen senx = 0, y se lo quitamos a los reales:
- senx = 0 ⇒ x = arc sen(0) ⇒ x = k π donde k ∈ ℤ,
- entonces, Domf = ℛ - {k π} con k ∈ ℤ
o también así: Domf = ℛ - {..., -3π, -2π, -π, 0, π, 2π, 3π, ...}
-
lbp_14
el 10/5/17Hola Unicoos, me dicen si tengo algún fallo en estos dominios, dudo en la última, porque creo que es todo R porque es un polinomio aunque tenga raíz pero no estoy segura, si me lo pueden justificar se lo agradecería mucho.
Muchas gracias
Neofito 007
el 10/5/17Requiere un poco de teoría elemental que en el proceso vas ir aprendiendo
La primera es correcta
En la segunda debes conocer que el argumento del logaritmo (en cualquier base) es siempre positivo, entonces
- 3x + 2 > 0 , allí encuentras el dominio
En el tercero, lo ya conocido denominador diferente de cero hay que resolver Ln(x-1)=0 cuya solución es x=2 , este valor se debe excluir.
Además el argumento debe ser positivo entonces
x - 1 > 0 , de acá que x>1
Por lo tanto el dominio es
( 1 , infinito) - { 2}
En el último debes conocer que el argumento o lo que va dentro de una raíz de índice par debe ser no negativo ( positivo o cero)
Dado que es la única restricción entonces
Dom = [ 0 , infinito)
lbp_14
el 10/5/17
Neofito 007
el 10/5/17El logaritmo es cero ( en cualquier base) si el argumento es 1 por eso x-1=1 de donde x=2
O hacerlo por simple definición
Ln(x) = y si y solo si x = e^y
En el ejercicio
Ln(x-1)=0 entonces 1-x=e^0=1 , de allí que x=2
Ojo que vale para cualquier base, sino que pongo la base neperiana porque el ejercicio es asi
-
Julio Rojas
el 10/5/17 -
Camilo
el 9/5/17hola me ayudan a saber a que se refiere cuando dice dos ordenadas extremas? en este ejercicio:
Determinar la ecuación de una curva, sabiendo que su pendiente es 1 cuando 𝑥 = 0 y la longitud de un arco de la misma es numéricamente igual a la mitad del área comprendida entre dicho arco, el eje de abscisas y dos ordenadas extremas.
-
Bautista Addad
el 9/5/17Hola, me ayudan con este ejercicio de Álgebra? Gracias. Geometría analítica:
Hallar la ecuación de una recta que pase por A(4, -3) de manera que el área del triángulo determinado por la recta y los ejes coordenados sea 3 unidades cuadradas
Antonio Silvio Palmitano
el 9/5/17Por favor, verifica tu enunciado.
Si haces un gráfico cartesiano, verás que el triángulo está incluido en el cuarto cuadrante, y que su base tiene llongitud mayor que 4 y que su altura tiene longitud mayor que 3, por lo que su área es mayor que 4*3/2 = 6 unidades cuadradas.
Espero haberte ayudado.
-
andres
el 9/5/17 -
Guillem De La Calle Vicente
el 9/5/17En la serie
Estoy estudiando esta serie.
En particular, estoy viendo convergencia uniforme, y he encontrado a través de la prueba de raíz que la serie converge uniformemente en cualquier intervalo del tipo [0, a] con a <2.
Pero no sé cómo proceder para la convergencia uniforme con x <0? ¿Alguien quiere ayudarme?
David
el 12/5/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
