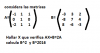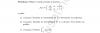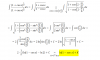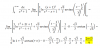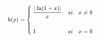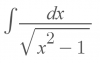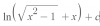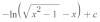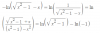Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Julio Rojas
el 27/4/17

buenas noches, tengo una pregunta rapida, en una integral es posible multiplicar y divir por X? estoy realizando un ejercicio y la unica manera para que me salga bien es haciendo eso

••0 voto/s
•
Antonio
el 27/4/17
sube el ejercicio
en un principio lo puedes hacer salvo que la x coja el valor 0

•0 voto/s
•

Cancelar
carla R
el 27/4/17

a duda es sobretodo en el apartado B
pero el resultado de a seria haciendo A^-1 AX+B B^-1 = A^-1 2A B^-1????? cuanto daria porque la inversa de B no me sale

••1 voto/s
•
Antonio
el 27/4/17
AX+B=2A
AX=2A-B
A^-1AX=A^-1(2A-B)
X=A^-1(2A-B)

•1 voto/s
•

Cancelar
carla R
el 27/4/17

en líneas generales se hacer estas ecuaciones de ALGEBRA, pero este es un peín más complicado. gracias

••1 voto/s
•
Antonio
el 27/4/17
Discutir sistema con dos parametros - ROUCHE
Discutir un sistema - Método de GAUSS
•1 voto/s
•

Cancelar
Natalia
el 26/4/17

me podeis ayudar con el c no tengo ni idea de como simplicas los logaritmos,creo que el proceso esta bien pero YO llego a : -in 5-5In6+ 6In -5In MUCHAS GRACIIAS

••0 voto/s
•
Ángel
el 27/4/17
En -1⁺: -ln6
En 0^-: -ln5
En el trozo de -1 a 0: -ln5-(-ln6)= -ln5+ln6= ln6-ln5= ln(6/5)

En 0⁺: ln5
En 1^-: ln6
En el trozo de 0 a 1: ln6-ln5= ln(6/5)

¹∫_-1 f(x) dx= ln(6/5)+ln(6/5)= 2ln(6/5)

•0 voto/s
•
Ángel
el 27/4/17

•0 voto/s
•

Cancelar
Apolinar
el 26/4/17

profesor de que forma puedo integrar ∫( (1+ cos x )^1/2 / (1- cos x )^1/2 ) dx , ME DIO Ln Ι csc x - cot x Ι + Ln Ι sen x Ι + c pero en el solucionario es ln Ι cos x -1I + C

••0 voto/s
•
Antonius Benedictus
el 27/4/17

•1 voto/s
•

Cancelar
Sebastian Canaviiri
el 26/4/17

me ayudan con estas derivadas por favor , gracias :)

••0 voto/s
•
Julian Jerez
el 26/4/17
Entiendo que en el primer punto todo esta dentro de la raiz, entonces
1). Derivada = (1/2(x^2+3x+1)^1/2)•(2x+3)= 2x +3 / 2(x^2+3x+1)^1/2
2). Derivada = (1/3(sinx)^2/3)•(cosx) = cosx/3(sinx)^2/3
3). Derivada = (e^{x^2})•(2x) = 2xe^{x^2}

•1 voto/s
•
Sebastian Canaviiri
el 27/4/17
Gracias crack

•0 voto/s
•

Cancelar
edith
el 26/4/17

Buenas noches. Alguien me ayuda con este problema? Tiene que salir 11/14 y me sale 7/28.
"Un examen de tipo test consta de 70 preguntas. Una alumna se sabe 50 preguntas de las 70. Si en cada pregunta hay cuatro posibles respuestas y sólo una es la correcta. ¿Cuál es la probabilidad de que elegida una pregunta al azar, dicha alumna la conteste acertadamente?"
Gracias

••0 voto/s
•
Antonio
el 26/4/17
Una pista:
Cuando le dan la pregunta puede ser que se la sepa o no.
si no se la sabe, la contestará al azar

•1 voto/s
•
Ángel
el 27/4/17
De las 70 preguntas:
*Se sabe 50= 50 acertará previsiblemente
*No se sabe 20 (tiene P=1/4 de acertar)= 20*1/4= 5 acertará previsiblemente
Si se elige al azar la pregunta, acertará (50+5)/70= 55/70= 11/14

•1 voto/s
•

Cancelar
Orianna Marquez
el 26/4/17

AYUDA PORFAA
Buenas tengo una duda, es con una integral impropia, la hice pero segun el libro y el internet dan resultados distintos y a mi tambien me da otro resultado, aqui les dejo la foto y los resultados de cada uno.
Resultado del libro: π/2√3
Resultado de internet :2π/3√3
Mi resultado 4π/3√3

••0 voto/s
•
Antonius Benedictus
el 27/4/17
Coincido con internet:
Revisa la descomposición en fracciones elementales.

•0 voto/s
•
Orianna Marquez
el 27/4/17
pero no le da el resultado de internet, le esta dando 2π√3/9 y el resultado de internet es 2π/3√3

•0 voto/s
•

Cancelar
Guillem De La Calle Vicente
el 26/4/17

Estudia la continuidad de la función

••0 voto/s
•
Antonio
el 26/4/17
El dominio es para los mayores de -1
el límite por la izquierda del cero es -1 y por la derecha es 1

•0 voto/s
•
Antonio Silvio Palmitano
el 26/4/17
Observa que el dominio de la función es D = (-1,+∞), y observa que la expresión de la función puede ser escrita en tres trozos:
f(x) =
- ln(1+x)/x si - 1 < x < 0
1 si x = 0
ln(1+x)/x si x > 0
Luego, observa que el primer trozo es continuo en su porción de dominio,
observa que el tercer trazo es continuo en su porción de dominio,
por lo que queda por estudiar la continuidad en el punto de corte, consignado en el segundo trozo:
1°) f(0) = 1 (como indica el segundo trozo);
2°) Límites laterales (observa que son indeterminados, y que los resolvemos con la Regla de L'Hôpital):
Lím(x→0-) - ln(1+x)/x = aplicamos la regla = Lím(x→0-) - 1/(1+x) = - 1,
Lím(x→0+) ln(1+x)/x = aplicamos la regla = Lím(x→0-) 1/(1+x) = 1,
y como los límites laterales no coinciden, tenemos que Lím(x→0) f(x) no existe;
3°) luego concluimos que la gráfica de la función presenta una discontinuidad inevitable tipo salto en x = 0.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Usuario eliminado
el 26/4/17

Hola. Ya había hecho ésta pregunta con otro ejercicio pero ahora tengo otra duda respecto al MÉTODO DE EULER-Cálculo Integral de otros ejercicio.
Aplicando ésta fórmula, quise comprobar de nuevo que usando cualquiera de los dos signos, da la misma respuesta.
i) √ax2 + bx + c = ±√ax + t si a > 0.
Pero en este ejercicio específicamente no puedo hacerlo.¿pueden ayudarme? Gracias.
Rpsta1:
Rpsta2:
intenté demostrarlo así. Pero ln(-1)??????????

••0 voto/s
•
Antonius Benedictus
el 26/4/17
El argumento logarítmico que proviene de una integral lleva valor absoluto. Ten esto en cuenta al evaluarlo.

•0 voto/s
•
Usuario eliminado
el 27/4/17
Gracias. Si, ya me di cuenta. Siempre debe ser positivo.

•0 voto/s
•

Cancelar