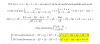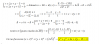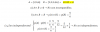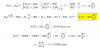-
Como resolveria esto
Limite cuando n tiene a infito(es una sucesión) de (2n-5-raiz(4n^2-7n))
carlos
el 12/4/17Ángel
el 12/4/17carlos
el 12/4/17 -
Hola chicos, me preguntaba si podríais resolverme esta duda. En un problema de geometría, he hecho los dos primeros apartados, pero el c no se como hacer para que me de la solución. Me dan dos rectas, r y s, voy a poner los vectores directores y sus puntos:
Y me piden la recta perpendicular común a las dos, antes tenía que sacar k, que erea un valor de un punto y todo lo he hecho bien, también sé sacar el vector director de la recta perpendicular, pero no se sacr el punto de corte, lo hace con lamda y mu (no se como ponerlos aquí), y de ahí saca el pun to de corte que es(cinco cuartos, siete cuartos, un medio) El vector director lo saca y le sale -4(1,1,0) . Cuando saqué k en un apartado también ponía en las soluciones que eran coplanarias, si me pudierais decir también como saber si son coplanarias, paralelas perpendicular etc. estaría muy bien. Muchas gracias y un saludo.
-
Hola chicos. En este ejercicio me preguntan por la integral de esta función y estoy algo atascado, no sé si voy bien. Gracias.
-
1) Escribir las ecuaciones de las circunferencias de radio R=√(5) que son tangentes a la recta x-2y-1=0 en el punto (3,1).
2) Hallar la ecuación de la circunferencia que es tangente a las dos rectas paralelas 2x+y-5=0, 2x+y+15=0, a una de ellas en el punto (2,1).
-
Tengo una duda sobre probabilidad.
¿Por qué no se me cumple en este caso la regla: la probabilidad de la intersección de dos sucesos independientes es el producto de la probabilidad de cada uno de los sucesos?
-Tomando un ejercicio del libro de 2º Bachillerato Ciencias Sociales SM:
16. Se lanza un dado cúbico, con sus caras numeradas del 1 al 6, y se anota su puntuación.
Se consideran los sucesos:
A = “salir un número par”, B = “salir un número que es un divisor de 12”
a) ¿Son A y B sucesos incompatibles?
b) Calcula la probabilidad de A ∪ B.
Mirando el apartado B
b) P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = 3/6+5/6 – 3/6=5/6
Si se observan los sucesos de manera desarrollada, se ve clara que la intersección tiene una probabilidad de 3/6, puesto que A = {2, 4, 6}; B = {1, 2, 3, 4, 6} (A ∩ B) = {2, 4, 6}
Pero haciendo el calculo correspondiente a la probabilidad de la intersección de sucesos independientes, es decir, el producto entre la P(A) y P(B), no obtengo la misma probabilidad ya que:
(3/6)*(5/6)=15/36=5/12
¿Dónde estoy fallando?
Muchas gracias por vuestra atención
Antonius Benedictus
el 12/4/17María Flores
el 12/4/17Gracias por su respuesta.
Aun suponiendo lo que usted dice, que creo tener claro puesto el ejercicio que he propuesto muestra sucesos compatibles ya que posee una intersección no nula, y al tratarse de lanzar un dado se trata de sucesos independientes ya que el resultado obtenido al tirarlo una vez no condiciona el que pudiera obtener tirando otra segunda vez. Si hasta el momento lo que digo es cierto, y el ejercicio trata sucesos independientes, ¿por qué el producto de los sucesos no me da como resultado la intersección, siendo sucesos independientes?
¿No son por tanto independientes como digo? No llego a entender por qué la regla no se cumple
Muchas gracias de nuevo por su amabilidad.
María Flores
el 12/4/17Muchas gracias por su respuesta Don Antonio.
En resumen y como últimas cuestiones:
Me queda claro que este suceso no es independiente porque el producto de las probabilidades por independiente no es igual a la probabilidad de la intersección. Pero ahora, sin disponer de la definición de los sucesos, es decir: el ejercicio sólo me da la probabilidad que tienen los diferentes sucesos expresado en número, ¿Cómo calculo la probabilidad de la intersección en caso de no ser independientes puesto de serlo sería tan simple como efectuar el producto?
¿Podría usted además explicarme por qué no son independientes? No entiendo qué hace depender que al lanzar el dado una segunda vez obtenga un resultado condicionado por lo que obtuve la primera vez si realmente en esta segunda vez mi espacio muestral sigue siendo el mismo, todos los números del dado.
-
Tenemos un cultivo de bacterias en un laboratorio y sabemos que su crecimiento es exponencial. Después de 1 minuto había 800 bacterias y después de 2 minutos había 1.280 bacterias.
a) Di cuál es la fórmula de la función que representa el crecimiento del cultivo de bacterias.
b) ¿Cuántas bacterias hay después de 5 minutos?
c) Después de cuánto tiempo el número de bacterias será de 10.000? -
¿Por qué ningún estudiante obtuvo la respuesta correcta?
Le di el siguiente problema a los estudiantes:
Dos n x n matrices A y B son similares si existe una matriz no singular P tal que A = P⁻¹BP.
- Demostrar que si A y B son dos matrices n x n similares, entonces tienen el mismo determinante y la misma traza.
- Dé un ejemplo de dos 2 x 2 matrices A y B con el mismo determinante, misma traza pero que no son similares.
La mayoría de los 20 estudiantes obtuvieron la primera pregunta correcta. Sin embargo, casi ninguno de ellos encontró un contra-ejemplo correcto a la segunda pregunta. La mayoría de ellos dieron ejemplos de matrices que tienen el mismo determinante y la misma traza.
Pero los cálculos muestran que sus ejemplos son matrices similares. Ellos no se molestaron en comprobar que, aunque, por lo que sólo trató de matrices al azar con la misma traza y el mismo determinante, con la esperanza de que sería un ejemplo correcto.
Pregunta: ¿cómo explicar que ninguno de los ensayos aleatorios dio matrices no similares?
Cualquier respuesta basada en la densidad o teoría de la medida está bien. En particular, puede asumir cualquier distribución razonable en las entradas de la matriz. Si importa, el curso se trata de matrices con coeficientes reales, pero puede suponer coeficientes enteros, ya que al elegir números al azar, la mayoría de la gente elegirá números enteros.
-
Diaz Daniel Victor
el 12/4/17Antonio Silvio Palmitano
el 12/4/17Vamos con una ayuda:
a) Para calcular el ingreso (I):
I = 300x + 900 y, luego sustituyes la expresión de y en función de x que tienes en el enunciado, y queda:
I(x) = 300x + 900*(23 - 5x)/(10 - x), con 0 < x < 23/5.
b) Planteamos la expresión de la función derivada:
I ' (x) = 300 + 900*( -5*(10 - x) - (23 - 5x)*(-1) )/(10 - x)2
reducimos el agrupamiento en el segundo término y queda:
I ' (x) = 300 + 900*(- 27 )/(10 - x)2 resolvemos numeradores en el segundo término y queda:
I ' (x) = 300 - 24300/(10 - x)2
luego planteamos la condición de punto crítico (posible máximo o posible mínimo):
I ' (x) = 0, sustituimos y queda:
300 - 24300/(10 - x)2 = 0, hacemos pasaje de término y queda:
300 = 24300/(10 - x)2 hacemos pasaje de divisor como factor y queda:
300*(10 - x)2 = 24300, hacemos pasaje de factor como divisor y queda:
(10 - x)2 = 81, hacemos pasaje de potencia como raíz y quedan dos opciones:
a) 10 - x = - 9, de donde despejamos: 19 = x > 23/5 = 4,6, que no cumple la condición del enunciado,
b) 10 - x = 9, de donde despejamos: 1 = x, que si cumple con dicha condición;
luego, reemplazamos en la expresión de y, y queda:
y = (23 - 5*1)/(10 - 1) = 18/9 = 2;
y la expresión para el Ingreso queda:
I(1) = 300*1 + 900*(23 - 5*1)/(10 - 1) = 300 + 900*18/9 = 300 + 1800 = 2100;
y para visualizar que el ingreso es máximo, puedes evaluar para valores cercanos a x = 1, por ejemplo:
I(0,9) = 300*0,9 + 900*(23 - 5*0,9)/(10 - 0,9) = 270 + 900* 18,5/9,1 = 270 + 1829,67 = 2099,67 < 2100,
I(1,1) = 300*1,1 + 900*(23 - 5*1,1)/(10 - 1,1) = 330 + 900*17,5/8,9 = 330 + 1769,66 = 2099,66 < 2100.
Luego, concluimos:
si se venden x = 1 tonelada de acero de baja calidad e y = 2 toneladas de acero de alta calidad, se obtiene un ingreso máximo I = 2100 euros.
Espero haberte ayudado.