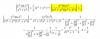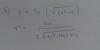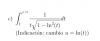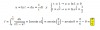-
lbp_14
el 20/3/17Hola Unicoos, alguien podría representarme gráficamente el planteamiento de este enunciado?
Muchas gracias
Antonio Silvio Palmitano
el 21/3/17Tenemos los puntos: P(4,2), Q(-2,5), y el punto genérico perteneciente al lugar geométrico: X(x,y).
Luego, planteamos las distancias entre el punto genérico y cada uno de los puntos, elevadas al cuadrado:
d(P,X)2 = (x - 4)2 + (y - 2)2 = x2 - 8x + 16 + y2 - 4y + 4 = x2 + y2 - 8x - 4y + 20,
d(Q,X)2 = (x + 2)2 + (y - 5)2 = x2 + 4x + 4 + y2 - 10y + 25 = x2 + y2 + 4x - 10y + 29.
Luego planteamos la condición que cumplen los puntos que pertenecen al lugar geométrico (observa que tenemos dos opciones):
1)
d(P,X)2 - d(Q,X)2 = 15, sustituimos expresiones y queda:
x2 + y2 - 8x - 4y + 20 - (x2 + y2 + 4x - 10y + 29) = 15, distribuimos el signo en el agrupamiento y queda:
x2 + y2 - 8x - 4y + 20 - x2 - y2 - 4x + 10y - 29 = 15, reducimos términos semejantes (observa que tenemos cancelaciones) y queda:
- 12x + 6y - 9 = 15, hacemos pasajes de términos, reducimos términos semejantes y queda:
6y = 12x + 24, dividimos en todos los términos de la ecuación por 6 y queda:
y = 2x + 4, que es la ecuación cartesiana explícita de una recta con pendiente m = 2, que pasa por el punto A(0,4).
2)
d(Q,X)2 - d(P,X)2 = 15, sustituimos expresiones y queda:
x2 + y2 + 4x - 10y + 29 - (x2 + y2 - 8x - 4y + 20) = 15, distribuimos el signo en el agrupamiento y queda:
x2 + y2 + 4x - 10y + 29 - x2 - y2 + 8x + 4y - 20 = 15, reducimos términos semejantes (observa que tenemos cancelaciones) y queda:
12x - 6y + 9 = 15, hacemos pasajes de términos, reducimos términos semejantes y queda:
- 6y = - 12x + 6, dividimos en todos los términos de la ecuación por - 6 y queda:
y = 2x - 1, que es la ecuación cartesiana explícita de una recta con pendiente m = 2, que pasa por el punto B(0,-1).
Luego, tenemos que los puntos del lugar geométrico forman las dos rectas paralelas, por lo que concluimos:
L = { (x,y) ∈ R2 / y = 2x + 4 ∨ y = 2x - 1 }.
Espero haberte ayudado.
-
Matías Ignacio Loyola Galdames
el 20/3/17 -
Adnan
el 20/3/17Tengo fallos al calcular estas derivadas
, pero no se cuáles
Sarqui
el 20/3/17en el c) no te has equivocado, estan bien hechos los cálculos pero se puede poner de forma más arreglada usando una fórmula trigonométrica que se estudia en 1ºBachillerato. Y en el b, lo que va en el numerador es la derivada de la raiz, pues f(x) es la raiz. Te adjunto foto de ambas resueltas para que lo veas, si tienes alguna duda, no dudes en preguntarme :)
-
carlos
el 20/3/17Hola, buenas tardes. Es la primera vez que entro, a ver si me podeis ayudar con este ejercicio
Un triángulo isósceles tiene por lados iguales AB y AC. Los vértices B y C se hallan sobre la recta r : x+3y-13=0. Las coordenadas de los vértices A y B son A (5,6) y B (-2,5). Halla las coordendas del vértice C y el área del triángulo
-
Sergi Raga
el 20/3/17
Hola podéis hacerme el E.X.7, el ejercicio 2
Guillem De La Calle Vicente
el 20/3/17El ejercicio siempre dicta lo que debemos hacer
cierto número es x y la suma de su inverso que es 1/x es 26/5
por lo tanto
x+1/x=26/5
(x^2+1)/x=26/5
5(x^2+1)=26x
5x^2+5=26x
5x^2-26x+5=0
aquí factoramos
(5x-25) (5x-1) / 5
(x-5) (5x-1)
aquí vemos que
x=5
x2=1/5
y reemplazado en la ecuación inicial tenemos que la respuesta es 5
porque
5+1/5=26/5 -
Alicia Díaz
el 20/3/17 -
Diego Martin Calzada
el 20/3/17¿Podrían explicar las ecuaciones racionales?
Ángel
el 20/3/17 -
Emilio Garcia Sánchez
el 20/3/17Hola,necesito ayuda con las funciones a trozos... otro video que me aclare
Ángel
el 20/3/17
-
Teresa
el 20/3/17Hola es en relación a matemáticas de 1 eso. Cómo se sabe cuando una relación de magnitudes es función. Gracias
Ángel
el 20/3/17Una función es una relación entre dos magnitudes, de tal manera que a cada valor de la primera le corresponde un único valor de la segunda, llamada imagen.
http://www.vitutor.com/fun/1/a_6.html
-
Nicolás Castillo
el 20/3/17
