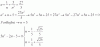Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Usuario eliminado
el 27/2/17

Como resuelvo esta ecuación?
4^x + 2^x+1 = 80

••0 voto/s
•
Antonius Benedictus
el 27/2/17
Cambio de variable: 2^x =y

•1 voto/s
•
Marcos
el 27/2/17

•1 voto/s
•

Cancelar
Usuario eliminado
el 27/2/17

Ayudadme!
La suma de un número, su inverso y el quíntuplo del cuadrado del inverso es 27/5. Encuentra el número

••0 voto/s
•
César
el 27/2/17
n+1/n+5(1/n)^2=27/5
n=5 , las opreaciones para ti vale.
salen dos soluciones mas pero no son numeros naturales

•0 voto/s
•
Usuario eliminado
el 27/2/17
Me lo podría resolver? Es que no me da 5...

•0 voto/s
•
César
el 27/2/17
Va Judiht

•0 voto/s
•

Cancelar
Usuario eliminado
el 27/2/17

como resuelvo estas ecuaciones?
a) ln (x+1)=2
b) x= raíz cuadrada de 2 + raíz cuadrada de 2 + raíz cuadrada de 2 (las raíces están juntas no separadas)
c) x= raíz cúbica de 6 + raíz cúbica de 6 + raíz cúbica de 6 (las raíces están juntas no separadas)

••0 voto/s
•
Antonius Benedictus
el 27/2/17
Foto original, por favor. Y algo de trabajo hecho.

•0 voto/s
•
Ángel
el 27/2/17
ln(x+1)=2
conviertes el 2 en ln:
ln(x+1)= ln e2
eliminas ln a ambos lados:
x+1= e2
despejamos x:
x=e2-1

•0 voto/s
•

Cancelar
María
el 27/2/17

••0 voto/s
•
Guillem De La Calle Vicente
el 27/2/17

•0 voto/s
•

Cancelar
ViRR
el 27/2/17

Buenas tardes, no sé cómo hacer este ejercicio:
Halla la ecuación de las elipses centradas en el origen:
a) Cuya distancia focal es 4 y la suma de distancias de un punto cualquiera a los focos es 8.
b) Sabiendo que A(0,5) y F(0,4).
c) Sabiendo que pasa por los puntos (2+√3 , 4) y (3, 3+√2).
¡Muchísimas gracias! :)

••0 voto/s
•
Antonius Benedictus
el 27/2/17
Elipse
•0 voto/s
•
Antonius Benedictus
el 27/2/17
Mira, haz algo y comentamos.
Fórmulas: http://www.vitutor.com/geo/coni/g_1.html

•0 voto/s
•
ViRR
el 27/2/17
El apartado a) me sale: x²/16 + y²/12=1.
El apartado b) me sale: x²/9 + y²/25=1.
Y el apartado c) no sé cómo hacerlo.

•0 voto/s
•
Antonius Benedictus
el 27/2/17
Pon foto del enunciado original y te lo corrijo.

•0 voto/s
•
ViRR
el 27/2/17
No se cargan las imágenes, así que te escribo lo que he hecho:
a) Distancia focal = 4 = 2c --> c=2
d(P,F) + d(P,F') = 2a --> 8 = 2a --> a=4
b²=a²-c²--> b²=12
Sol.: x²/16 + y²/12 = 1
b) F(0,4) --> F(c,0) --> c=4 // A(0,5) --> a=5
b²=a²-c²--> b²=9
Sol.: x²/9 + y²/25 = 1

•0 voto/s
•

Cancelar
maria belen
el 27/2/17

dominio recorrido y todas las caracteristicas de las funciones porfavor¡¡¡¡¡¡¡¡¡¡es para un examen mañana

••0 voto/s
•
Antonius Benedictus
el 27/2/17
Representación de funciones Representación de funciones
•0 voto/s
•

Cancelar
Ángela
el 27/2/17

Estudia segun los valores de a el rango de la matriz:
1 -1 1
3 1 a
2 2 1
Yo he observado que la si a vale 2 seria combinacion lineal de la primera y tercera fila, pero si no me diera cuenta de eso, como se haria?

••0 voto/s
•
Antonius Benedictus
el 27/2/17
Mira el ejercicio inmediatamente inferior (Vanesa)

•0 voto/s
•

Cancelar
Vanesa
el 27/2/17
1. Dada la matriz determinar el/los valor/es del parámetro k por los cuales la matriz tiene rango 2.
Me podéis ayudar con esto?
••0 voto/s
•
César
el 27/2/17

•1 voto/s
•
Antonius Benedictus
el 27/2/17

•1 voto/s
•
Antonio
el 27/2/17
En primer lugar, tienes que comprobar que el rango de la matriz dada no es 3, es decir, que el determinante de la matriz 3x3 es 0, pues de lo contrario el rango sería 3.
En segundo lugar, tienes que encontrar un menor distinto de 0, es decir una matriz 2x2, cuyo determinante sea distinto de 0.

•1 voto/s
•

Cancelar
Leticia
el 27/2/17

He visto los vídeos de radicales ,y la verdad es que tengo bastantes dudas acerca la resolución de este ejercicio de simplificación de radicales. Gracias de antemano.

••0 voto/s
•
Antonio Silvio Palmitano
el 27/2/17
Comencemos por desarrollar el numerador (N) y resolver el denominador (D) por separado:
N = ( 2√(24) - √(48) )( √(6) + √(3) ) = distribuimos = 2√(24*6) + 2√(24*3) - √(48*6) - √(48*3) = 2√(144) + 2√(72) - √(288) - √(144) = resolvemos y factorizamos argumentos:
= 2*12 + 2√(36*2) - √((144*2) - 12 = resolvemos y distribuimos raíces = 24 + 2*6√(2) - 12*√(2) - 12 = resolvemos en el segundo término:
= 24 + 12√(2) - 12*√(2) - 12 = resolvemos y cancelamos términos opuestos = 12;
D = 7√(3)*4√(12)/14 = resolvemos y asociamos raíces = 28√(36)/14 = simplificamos y resolvemos = 2*6 = 12.
Luego, tienes para la expresión del enunciado:
( 2√(24) - √(48) )( √(6) + √(3) ) / ( 7√(3)*4√(12)/14 ) = reemplazamos = 12 / 12 = 1.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Julio
el 27/2/17

HOLA, me podrían ayudar con el 2, grcaias

••0 voto/s
•
Antonius Benedictus
el 27/2/17

•0 voto/s
•

Cancelar