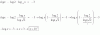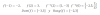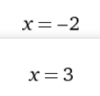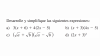https://www.symbolab.com/solver/step-by-step/ln%20x%20-ln%202%20%5Ccdot%5Clog_%7B%5Csqrt%7B2%7D%7D%5Cleft(x%5Cright)%3D-3 

RAZON DE CAMBIO 02 Razon de Cambio 01

x (lado de la base)  y  h (altura)

x^2 h=2

h=2/x^2 

S=x^2+4xh=x^2 + 4x(2/x^2)= x^2 +(8/x)

¿Darío, en qué Universidad española preguntan esto?

Dominio de una funcion

a)

Observa que a la función le corresponde una expresión algebraica fraccionaria, por lo que planteamos que el denominador debe ser distinto de cero:

x² + x - 2 ≠ 0, luego observa que en el primer miembro tenemos un polinomio cuadrático, lo factorizamos y queda:

(x - 1)(x + 2) ≠ 0, luego observa que para que el producto sea distinto de cero debe cumplirse que ambos factores deben ser distintos de cero, por lo que planteamos:

x - 1 ≠ 0, de donde tenemos: x ≠ 1,

x + 2 ≠ 0, de donde tenemos: x ≠ -2.

Luego, concluimos que el dominio de la función es: D_f = R - {-2,1}.

b)

Observa que el numerador está definido para todos los números reales (observa que la raíz cúbica, como todas las raíces con índice impar, no tiene restricciones para su argumento), y que el denominador es estrictamente mayor que cero para todo número real (observa que es una suma de términos positivos, ya que el primero es un cuadrado y el segundo es 1).

Luego, concluimos que el dominio de la función es: D_g = R.

c)

Observa que en ambos términos de la expresión de la función tenemos raíces cuadradas, por lo que planteamos que sus argumentos deben ser ambos mayores o iguales que cero:

4 - x ≥ 0, hacemos pasaje de término y queda: - x ≥ - 4, multiplicamos en ambos miembros por -1 (observa que cambia la desigualdad) y queda: x ≤ 4,

que corresponde al intervalo: (-∞,4] (1);

x² - 1 ≥ 0, hacemos pasaje de término y queda: x² ≥ 1, hacemos pasaje de potencia como raíz (observa que el exponente es par, por lo que su base puede ser positiva o negativa):

|x| ≥ 1, que corresponde al intervalo: (-∞,-1] ∪ [1,+∞) (2).

Luego, planteamos la intersección entre los intervalos señalados (1) (2), y concluimos que el dominio de la función es: D_h = (-∞,1] ∪ .[1,4].

Espero haberte ayudado.

Factoriza el polinomio por Ruffini:

Iguala cada factor a 0. La ecuación de 2º grado no tiene solución real.

Observa que x = 3 es una raíz de la ecuación y que - 2 es otra de sus raíces, por lo que aplicas la Regla de Ruffini en forma sucesiva y tienes:

     1     0    -6    -7    -6

 3         3     9     9     6

     1     3     3     2     0  

-2       -2    -2   -2

     1     1     1    0

luego, observa que el cociente queda: C(x) = x² + x + 1, cuyas raíces son complejas y que las puedes calcular con la fórmula resolvente para ecuaciones polinómicas cuadráticas y quedan: x = (-1 ±√(3)i)/2.

Luego, la ecuación del enunciado factorizada en el campo de los números reales queda:

(x - 3)(x + 2)(x² + x + 1) = 0, y sus raíces reales son: x₁ = 3 y x₂ = -2.

Luego, la ecuación del enunciado factorizada en el campo de los números complejos queda:

(x - 3)(x + 2)( x - (-1 +√(3)i)/2 )( x - (-1 -√(3)i)/2 ) = 0, y sus raíces son: x₁ = 3 y x₂ = -2, x₃ = (-1 +√(3)i)/2 y x₄ = (-1 -√(3)i)/2.

Espero haberte ayudado.

1°) Puedes comenzar por revisar los múltiplos comunes de 54 y de 72 (consignamos la cantidad de pisadas en la tercera línea):

0    54               108               162    216    270               324                378    432    486                540                594    648    702  ...                                     2160    2214

0               72               144               216              288                360                432               504                576               648               720 ...                           2160                2232

0      1        2      3        4          5        6         7        8        9        10      11        12       13      14        15       16      17       18       19      20 ....                             60        61        62   

Observa que la cantidad de pisadas cuando coinciden con un múltiplo de 216 (216*1, 216*2, 216*3, etc) es el múltiplo correspondiente de 6 (6*1, 6*2, 6*3, etc),

luego, si quedaron marcadas 61 pisadas tenemos:

61 = 60 + 1 = 6*10 + 1,

y observa que el décimos múltiplo de 216 es: 216*10 = 2160,

y observa que al siguiente múltiplo de 216 le sigue un múltiplo de 54,

por lo tanto tenemos para el largo del terreno:

L = 216*10 + 54 = 2160 + 54 = 2214 cm = 22,14 m.

Hemos agregado a la tabla de múltiplos las columnas correspondientes a las respuestas.

Espero haberte ayudado.

2°) Observa que si mides de dos en dos y sobra uno, tienes que la longitud de la cuerda es un número impar,

y observa que si mides de tres en tres y sobran dos, tienes que la longitud es un número impar que excede en dos a un múltiplo impar de tres, por lo que tienes hasta ahora como posibles longitudes:

L =     5      11     17    23     29    35     41    47    53    59    65     71     77     83    89    95.

Luego, observa que si mides de cuatro en cuatro y sobran tres, tienes que la longitud es un número impar que excede en tres a un múltiplo de 4 (7, 11,15,19,23,27,31, ....),

luego descartamos de la lista señalada (1) a los números que no cumplan esta condición y las posibles longitudes quedan:

L = 11     23     35     47     59    71    83    95 (2)

Luego, observa que si mides de cinco en cinco y sobran cuatro, tienes que la longitud es un número impar que excede en cuatro a un múltiplo impar de 5 (9, 19, 29, ...),

luego descartamos de la lista señalada (2) a los números que no cumplan esta condición y la posible longitudes queda:

L = 59 metros,

luego, observa que si divides a 59 por 6, tienes que el cociente es 9 y el resto es 5, por lo que se cumple la última condición.

Espero haberte ayudado.

Observa que a las 8 la noticia es conocida por 3 personas,

y observa que a las 8:30 la noticia es conocida por 3*3 = 9 personas más, lo que totaliza 12 personas,

y observa que a las 9 la noticia es conocida por 12*3 = 36 personas más 

y así sucesivamente, y observa que por cada media hora que pasa la cantidad de nuevas personas que conoce la noticia se incrementa en el triple de la cantidad anterior.

Luego hacemos una tabla, en la que consideramos t = 0 a las 8 horas y llamamos N a la cantidad de personas que conocen la noticia hasta ese momento:

  t                 N

 0                 3

1/2         3 + 3*3 = 3 + 9 = 12

 1           12 + 3*12 = 12 + 36 = 48

3/2        48 + 3*48 = 48 + 144 = 192

 2           192 + 3*192 = 192 + 576 = 768

5/2        768 + 3*768 = 768 + 2304 = 3072

Luego, observa que transcurridas 2 horas tienes que 768 personas conocen la noticia, y observa que transcurridas 2 horas y media (5/2 hora) la noticia ya es conocida por toda la población, ya que la cantidad N excede a la cantidad de personas del pueblo.

Por lo que concluimos que la totalidad del pueblo conoce la noticia entre las 10 y las 10:30 horas.

Espero haberte ayudado.

Hola Paula estas son las respuestas:

a) 3x+18+8x-20 ;        11x-2

b) 4x²-5x+12x-15;       4x²+7x-15

c) (√a)²-  ( √a •√b) • (√b •√a) - (√b)² ;    a - (√a•b)² -b;      a - ab - b

d) Identidad notable :  4x² + 12x + 9

El c) no es correcto.