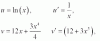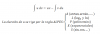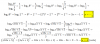-
Marta
el 4/2/17
Como hago esta integral?
Enrique Sánchez Sancho
el 4/2/17 -
Enrique Sánchez Sancho
el 4/2/17 -
Marta
el 4/2/17(function(){var g=this;function h(b,d){var a=b.split("."),c=g;a[0]in c||!c.execScript||c.execScript("var "+a[0]);for(var e;a.length&&(e=a.shift());)a.length||void 0===d?c[e]?c=c[e]:c=c[e]={}:c[e]=d};function l(b){var d=b.length;if(0=d.offsetWidth&&0>=d.offsetHeight)a=!1;else{c=d.getBoundingClientRect();var f=document.body;a=c.top+("pageYOffset"in window?window.pageYOffset:(document.documentElement||f.parentNode||f).scrollTop);c=c.left+("pageXOffset"in window?window.pageXOffset:(document.documentElement||f.parentNode||f).scrollLeft);f=a.toString()+","+c;b.b.hasOwnProperty(f)?a=!1:(b.b[f]=!0,a=a<=b.g.height&&c<=b.g.width)}a&&(b.a.push(e),b.c[e]=!0)}p.prototype.checkImageForCriticality=function(b){b.getBoundingClientRect&&q(this,b)};h("pagespeed.CriticalImages.checkImageForCriticality",function(b){n.checkImageForCriticality(b)});h("pagespeed.CriticalImages.checkCriticalImages",function(){r(n)});function r(b){b.b={};for(var d=["IMG","INPUT"],a=[],c=0;c
-
Enrique Sánchez Sancho
el 4/2/17∫ ( 12 + 3x3 ) lnx dx , Sería por udv -∫ uv v du ¿?¿ La u es el polinomio y la v seria el ln x?
-
Usuario eliminado
el 4/2/17
-
Manuel
el 4/2/17Ayuda con estos ejercicios, Antonio Benito. ¡PASO A PASO, POR FAVOR! Lo necesito lo más desarrollado posible.
Gracias de antemano. Un saludo.
Manuel
el 4/2/17 -
Enrique Sánchez Sancho
el 4/2/17La integral de ∫ (cos 3x ) / (1+sen 3x ) 5 dx Siendo el cambio de variable 1 +sen 3x = t
Antonio Silvio Palmitano
el 4/2/17Has planteado bien el cambio de variable, luego tienes: 3cos(3x)dx = dt, de donde puedes despejar: cos(3x)dx = dt/3,
luego pasamos a la integral:
I = ∫ (cos 3x ) / (1+sen 3x ) 5 dx, ordenamos factores en el argumento de la integral y queda:
I = ∫ 1/(1+sen 3x )5 (cos 3x ) dx, sustituimos y queda:
I = ∫ (1/t5)*(dt/3) = (1/3) * ∫ t-5dt, y puedes continuar la tarea.
Espero haberte ayudado.
Enrique Sánchez Sancho
el 4/2/17 -
Manuel
el 4/2/17 -
Manuel
el 4/2/17 -
Bet
el 4/2/17
Buenas, cómo puedo determinar si una función es inyectiva o epiyectiva si están escritas (así como se muestran en esos ejercicios) y no en una gráfica?
Gracias de antemano
Antonio Silvio Palmitano
el 4/2/1714)
I) Inyecitvidad: consideramos x1 y x2 pertenecientes a R, y x1 ≠ x2. Luego planteamos:
x1 ≠ x2 , multiplicamos por 1/3 en ambos miembros de la igualdad negada:
x1 /3 ≠ x2 / 3 , restamos 5 en ambos miembros de la igualdad negada:
x1 /3 - 5 ≠ x2 / 3 - 5 , sustituimos expesiones:
g(x1) ≠ g(x2), por lo que concluimos que la función g es inyectiva.
II) Epiyectividad: llamamos g(x) = y. Luego planteamos:
g(x) = y, sustituimos la expresión de la función:
x/3 - 5 = y, hacemos pasaje de término:
x/3 = y + 5, multiplicamos por 3 en todos los términos de la ecuación:
x = 3y + 15, por lo que tenemos que para cada valor y real existe un valor x real y la función g es epiyectiva.
III) Como la función es inyectiva y también epiyectiva, decimos que es biyectiva y que admite función inversa y, para hallar la expresión de la función inversa, permutamos variables en la última ecuación remarcada y queda:
y = 3x + 15, por lo que la expresión de la función inversa queda: g-1(x) = 3x + 15, con dominio R e imagen R.
Por lo tanto, concluimos que las opciones I) y II) son verdaderas, y la opción III) es falsa.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 4/2/1715)
Epiyectividad. Llamamos f(x) = y, luego sustituimos la expresión de la función y queda:
(4x + 3)/(x - 1) = y, hacemos pasaje de divisor como factor y queda:
4x + 3 = y(x - 1), distribuimos en el segundo miembro y queda:
4x + 3 = xy - y, hacemos pasajes de términos y queda:
4x - xy = - y - 3, extraemos factores comunes en ambos miembros y queda:
- x(- 4 + y) = - (y + 3), multiplicamos por -1 en ambos miembros, ordenamos términos en el agrupamiento del primer miembro y queda:
x(y - 4) = y + 3, hacemos pasaje de factor como divisor y queda.
x = (y + 3)/(y - 4), observa que debe cumplirse: y - 4 ≠ 0, lo que conduce a: y ≠ 4,
por lo que concluimos que para que la función f sea epiyectiva, debe tener codominio: B = R - {4},
por lo que la opción A es la respuesta correcta.
Espero haberte ayudado.
