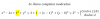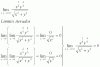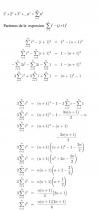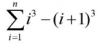Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Carlos Ojeda
el 4/1/17

Hola Unic@@s, ¿me ayudan con estos dos ejercicios de inducción? en el primero ya véis dónde me he quedado Gracias

••0 voto/s
•
Antonius Benedictus
el 4/1/17

•1 voto/s
•
Antonius Benedictus
el 4/1/17
En el primero la inducción empieza en n=2.

•1 voto/s
•

Cancelar
Gerardo
el 4/1/17

Hola buen dia espero me puedan orientar a cerca de este problema de algebra. Se trata a cerca de determinantes.
Si |a b c| | 2a 2b 2c |
A= |p q r | =2 , calcule | 2p+x 2q+y 2r+z |
| x y z | | -x -y -z |
Recuerdo que para calcular el determinante se tomaba en cuenta el determinante de la matriz A, según yo y mis cuentas me salía que:
2( siendo el determinante de la matriz A) * (2)* (2) *( - ) = -8
Entonces el determinante de la segunda matriz es = -8 Si estoy bien?? o estoy confundiendome?
Se los agradeceria mucho :D

••0 voto/s
•
Antonio Silvio Palmitano
el 4/1/17
Recuerda que un factor común en una fila (o columna) puede ser extraído como factor fuera del determinante.
Recuerda que si una fila es una suma (o resta) de términos, el determinante puede ser descompuesto como suma de determinantes, con uno de los términos de la fila en cada determinante, y con las demás filas sin alterarlas.
Recuerda que si un determinante tiene dos filas iguales (o dos columnas iguales), entonces el determinante es igual a cero.
1) Extraemos factor común 2 en la primera fila, y extraemos factor común -1 en la tercera fila y el determinante queda:
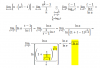
| a b c |
D = 2*(-1) * | 2p+x 2q+y 2t+z |
| x y z |
2) Descomponemos el determinante como la suma de dos determinantes, cada uno con la misma fila 1 y la misma fila 3, pero con uno de los términos de la fila 2 para cada uno:
D = -2*(D₁ + D₂) (*)
3) Planteamos los determinantes secundarios:
| a b c | | a b c |
D₁= | 2p 2q 2t | = extraemos factor común en la fila 2 = 2 * | p q r | = 2*2 = 4
| x y z | | x y z |

| a b c |
D = | x y z | = observa que la fila 2 y la fila 3 son iguales = 0.
| x y z |
4) Reemplazamos en la expresión señalada (*) y llegamos a:
D = -2*(4 + 0) =- 8.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
Julio Rojas
el 3/1/17

hola, estuve intentando pero no se como resolver este ejercicio de limites

••0 voto/s
•
Antonius Benedictus
el 3/1/17
El límite pedido no existe, La función oscila entre -2 y 2.

•0 voto/s
•

Cancelar
Carlos Ojeda
el 3/1/17

Hola, tengo una duda con este ejercicio de multiplicadores de Lagrange, ¿sabéis qué procedimiento se sigue para expresar el círculo en forma canónica? Gracias

••0 voto/s
•
Antonius Benedictus
el 3/1/17

•1 voto/s
•

Cancelar
XOK
el 3/1/17

Holaa David puedes subir un vide de anova de un factor es de probabilidad graaciaas

••0 voto/s
•
Ángel
el 3/1/17
Supongo que serás universitari@, esto te ayudará:
http://networkianos.com/anova-de-un-factor-que-es-como-analizar/

•0 voto/s
•

Cancelar
Ylenia Montes
el 3/1/17

Me piden que halle el area comprendida entre y=e^x y la cuerda de la misma que tiene por extremos los puntos de abscisas 0,1.
Tengo una idea de como hacer este ejercicio, pero no sé si estará bien. ¿Alguien puede ayudarme? ¡Mil gracias!

••0 voto/s
•
Guillem De La Calle Vicente
el 3/1/17
Integral definida entre 0 y 1 de e^x

•1 voto/s
•
César
el 3/1/17
Va Ylenia

•1 voto/s
•
Antonio Silvio Palmitano
el 4/1/17
Recuerda que llamamos cuerda al segmento (trozo de recta) que une dos puntos de una curva, y llamamos arco al trozo de curva correspondiente.
Observa que los puntos de la gráfica de la función exponencial que son extremos de la cuerda son: A(0,1) y B(1,e), y la ecuación cartesiana explícita de la recta que la contiene tiene pendiente m = (e-1)/(1-0) = (e-1), y ordenada al origen b=1, por lo que la ecuación queda: y (e-1)x + 1.
Luego, si haces un gráfico cartesiano, observa que la cuerda se encuentra "más arriba" que el arco de curva exponencial, y que ambos tienen extremos en los puntos A y B.
Luego, el área de la región limitada por la cuerda y el arco de curva exponencial queda:
A = ∫ ( (e-1)x + 1 - e^x ) dx = [ (e-1)x²/2 + x - e^x ], evaluamos con la regla de Barrow entre 0 y 1 y queda:
A = ( (e-1)*1/2 + 1 - e ) - ( (e-1)*0/2 + 0 - 1 ) = e/2 - 1/2 + 1 - e + 1 = 3/2 - e/2 = (3 - e)/2 ≅ 0,1409.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
Usuario eliminado
el 3/1/17
Me pidieron resolver el lim de n(a^(1/n)-1) cuando n tiende a infinito, sin utilizar derivadas ni series, solo transformaciones algebraicas.
Transformaciones.
1. lim de (a^y-1)/y cuando y tiende a cero.
2. lim de (lna/lnp)(p-1) cuando p tiene a 1. (allí saque la constante Ln a)
3. Ln a por lim de (e^t-1)/t cuando t tiende a cero.
4. Ln a por lim de h/ln(h+1) cuando h tiende a cero.
No pude resolver ninguno, por ahora, apreciaria una mano o pista.
••0 voto/s
•
Antonius Benedictus
el 3/1/17

•1 voto/s
•
Usuario eliminado
el 4/1/17
Gracias Antonio, ¿no sabrias que libro puedo leer para aprender a tranformar las expresiones de esa forma en que lo haces? conozco las propiedades, pero hacer esa transformacion al pie de la letra deberia jamas me lo imaginaria.

•0 voto/s
•

Cancelar
Amanda
el 3/1/17

Me estoy intentando poner al día ahora con los problemas, ya que lo que son las fracciones en si, ya lo tengo controlado, a ver si me podéis ayudar con esta, porque no sé muy bien como hacerlo o en que consiste. El Lunes examen de fracciones ya.

Dos personas salen de Toledo con dirección a Burgos. Después de un cierto tiempo una de ellas ha recorrido 2/5 y la otra 1/4 ¿Quién está más cerca de Burgos? Razona tu respuesta.

Yo creo que ambas están igual de cerca...

••0 voto/s
•
Guillem De La Calle Vicente
el 3/1/17
La primera está más cerca porque ha recorrido 2/5 del recorrido (0,4) y la otra ha recorrido 0,25

•1 voto/s
•
Amanda
el 3/1/17
¿Y eso como lo puedo saber?

•0 voto/s
•
César
el 3/1/17
sabemos que 1/4<2/5, pues 1/4=0.25 y 2/5 =0.4 , luego ha recorrido mas distancia el que haya hecho 2/5 del camino.
Podemos hacerlo calculando em m.c.m y ponerlo como denominador
1/4 2/5 mcm(5,4)=20 1/4=5/20 2/5=8/20 como se ve es mayor 8/20

•1 voto/s
•
Guillem De La Calle Vicente
el 3/1/17
Haciendo la división de 2/5 y 1/4. Y observas que el 2/5 es mas grande, por lo tanto, habrá recorrido más trozo y eso implica que está más cerca de Burgos.

•1 voto/s
•
Amanda
el 4/1/17
Muchas gracias, ya no creo que se me olvide, o eso espero.

•0 voto/s
•

Cancelar
sara López
el 3/1/17

Hola alguien puede explicarme como hacer ese límite,
se supone que da 0.
lim(x,y)->(0,0) (x^2*y^2) /(sqrt(x^2+ y ^2))

••0 voto/s
•
Antonius Benedictus
el 3/1/17
¿Cuál de los dos, el escrito a máquina o el escrito a mano?

•1 voto/s
•
sara López
el 3/1/17
a mano es el mismo solo que si no lo exprese bien decidí ponerlo usarlo el paint.
Se puede usar usando restricciones de conjuntos? Podrias explicarme eso si no te importa? Gracias!!

•0 voto/s
•
Antonius Benedictus
el 3/1/17

•0 voto/s
•
César
el 3/1/17
con limites iterados

•0 voto/s
•
Lidia Anaya
el 3/1/17
hola césar, el que los dos límites iterados existan no implica que el límite exista.
Por ejemplo
lim_(x,y)->(0,0)xy /(x^2 + y ^2)

no existe, pero sus límites iterados sí.

•1 voto/s
•

Cancelar
Usuario eliminado
el 3/1/17

HOLA ALGUIEN ME PUEDE ECHAR UNA MANO CON LAS SERIES? EL PROBLEMA LO TENGO EN DEDUCIR EL TERMINO GENERAL.
AQUÍ OS PONGO TRES EJEMPLOS QUE NO ENTIENDO COMO LLEGAN AL TERMINO GENERAL, EN TEORIA SON LOS MÁS SENCILLOS:

••0 voto/s
•
César
el 3/1/17
Va Juan te hago el segundo
El primero no es mas que una progresion aritmetica

•1 voto/s
•
Usuario eliminado
el 4/1/17
Gracias por la respuesta, pero que quiere decir partimos con ?
Un saludo!

•0 voto/s
•

Cancelar