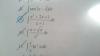-
Carlos Ojeda
el 28/12/16Hola, profesor Antonio Benito, me estoy volviendo loco con este ejercicio de diagonalización:
Logré resolver el apartado a), pero el que me está volviendo loco es el b), lo busqué resuelto, y sigo igual de loco xd , bien, mis dudas con esa resolución:Este es el apartado b) que no entiendo, abajo las dudas.
El único vector independiente es el (2,2,0,-2), eso lo entiendo, se le asignan parámetros a x,y,z y t, "t" se expresa en función de alfa y de beta porque la z es 0 en nuestra base ¿me equivoco?
Lo que yo no acabo de entender es porqué a la hora de expresar la base en función de esos parámetros, Vλ1 se pone e3 multiplicando por el parámetro (no sé cómo se llama xd) cuando e3 en la base es 0, ¿por qué lo ponen así? ¿es necesario expresar e4 en función de alfa y beta? y ya lo que no entiendo nada de nada al final, es donde pone base Vλ1 = { e1-e4,e2-e4,e3} mi dudas con esta: ¿de dónde viene e1 y e4, si vamos a expresar x en función del resto, ¿no sería e2 - e4? y e3 que sigo si entender por qué está ahí. Gracias!! y Feliz Navidad.
-
Andreea
el 28/12/16
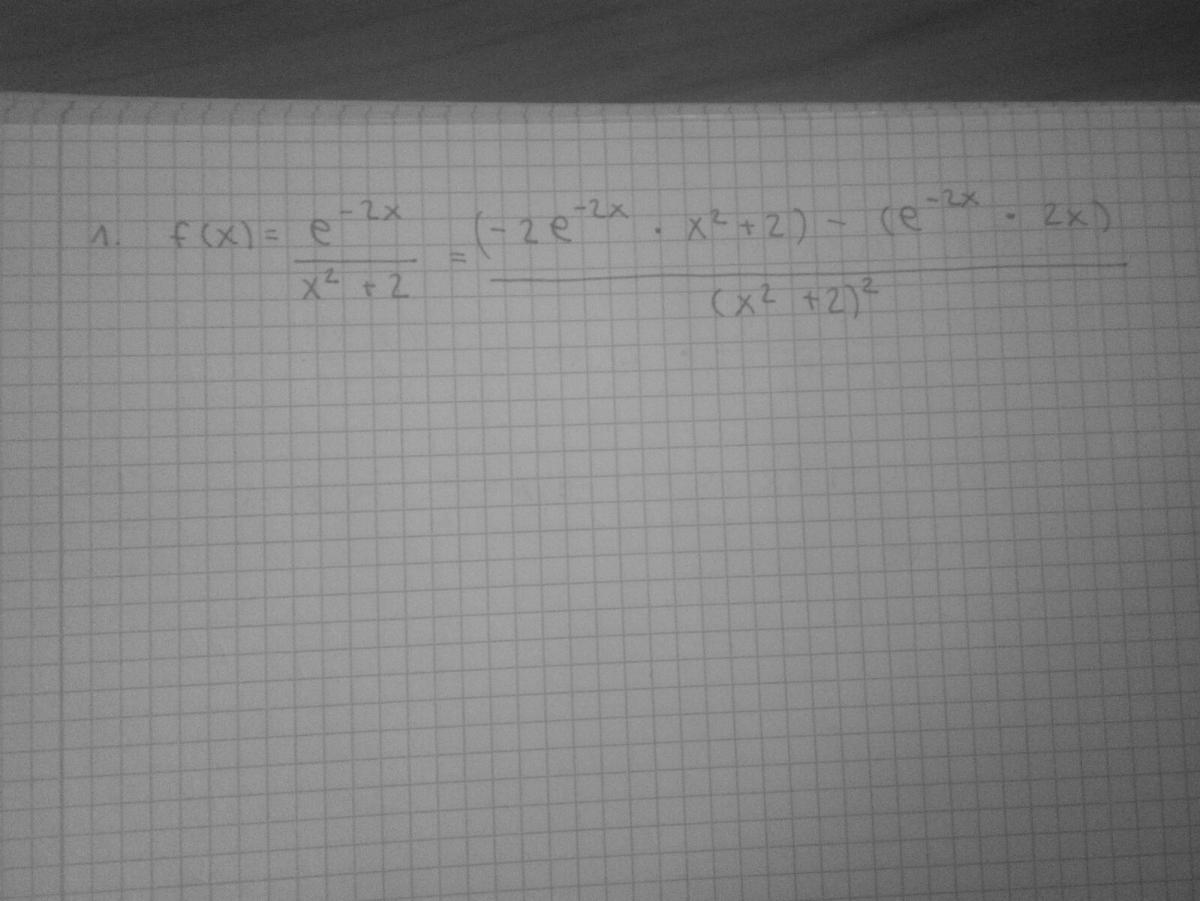Buenas! Estoy estudiando las derivadas y no me aclaro con las funciones de e. No se si tengo bien lo que he hecho hasta ahora y tampoco se como simplificarla...
Graciaaas !
Antonio Silvio Palmitano
el 28/12/16Si la expresión de la función es:
f(x) = e-2x/(x2 + 2),
observa que tienes un cociente (u/v), por lo que planteamos:
u = e-2x, cuya derivada queda (observa que debemos aplicar la regla de la cadena): u ' = e-2x(-2) = -2e-2x,
v = x2 + 2, cuya derivada queda: v ' = 2x.
Luego, aplicamos la regla de derivación de un cociente:
f ' (x) = ( u ' * v - u * v ' )/v2 = ( -2e-2x*(x2 + 2) - e-2x*(-2x) )/(x2 + 2)2, extraemos factor común en el numerador:
= -2e-2x(x2 + 2 - x)/(x2 + 2)2.
Espero haberte ayudado.
-
alberto
el 28/12/16En un ejercicio en el que nos piden una recta que pase por un punto y corte a dos rectas, ¿puede haber varias soluciones de esa recta pedida? Es decir, dependería de los diferentes vectores que formemos y demás procedimientos internos del ejercicio, ¿no?
Gracias de antemano.
-
carmen ruiz
el 28/12/16Ayuda!!!! pensaba que después de mil intentos la habia resuelto,pero va a ser que no:( (es la 9)
Antonio Silvio Palmitano
el 28/12/169) Observa que la expresión de la función a integrar puede simplificarse:
f(x) = (x2 + 2x + 1)/(x + 1) = factorizamos el numerador = (x + 1)2/(x + 1) = simplifiamos = x + 1.
Luego pasamos a la integral:
I = ∫ (x2 + 2x + 1)/(x + 1) dx = ∫ (x + 1)dx = ∫ xdx + ∫ 1dx = x2/2 + x + C.
Espero haberte ayudado.
-
Carlos
el 28/12/16Consulta, este ejercicio es una variable aleatoria continua o discreta y como puedo saber identificar eso
JUAN PABLO CUBAS
el 28/12/16X= {Peso en kilogramos}, es una variable aleatoria continua porque el peso no solamente es 1 kg, 2Kg,3kg,4kg,... sino tambien cualquier valor entre medias.
Ademas te dan una "funcion de densidad" lo que implica V.A continua
tambien te dan un intervalo par dicha funcion de densidad entre 1 y 4, lo que implica que la x puede tomar "cualquier valor en ese intervalo.
-
Carlos
el 28/12/16 -
Carlos Ojeda
el 28/12/16 -
Carlos
el 28/12/16Hola, me pueden ayudar con el punto C, se que para ver la homogeneidad es el coeficiente de variabilidad, pero no entiendo hasta y desde....
Antonio Silvio Palmitano
el 28/12/16Puedes calcular las varianzas y las desviaciones típicas para cada grupo, y observa que al grupo 1 le corresponden los cuatro primeros intervalos, y que al grupo 2 le corresponden los cinco últimos intervalos, y que para cada intervalo consideramos su valor medio.
Para el grupo 1:
Media: μ1 = ∑ xi * fi / ∑ fi = (15*3 + 25*5 + 35*10 + 45*11)/(3 + 5 + 10 + 11) = 1015/29 = 35.
Varianza: V1 = ∑ (xi - μ1)2 * fi / ∑ fi = ( (-20)2*3 + (-10)2*5 + (0)2*10 + (10)2*11 )/29 = 2800/29 ≅ 96,55.
Desviación típica: σ1 = √(V1) = √(2800/29) ≅ 9,83.
Para el grupo 2:
Media: μ2 = ∑ xi * fi / ∑ fi = (55*8 + 65*7 + 75*6 + 85*5 + 95*5)/(8 + 7 + 6 + 5 + 5) = 2245/31 ≅ 72,42.
Varianza: V2 = ∑ (xi - μ2)2 * fi / ∑ fi = ( (-17,42)2*8 + (-7,42)2*7 + (2,58)2*6 + (12,58)2*5 + (22,58)2*5 )/31 = 3028,7844/31 ≅ 97,70.
Desviación típica: σ2 = √(V2) ≅ √(3028,7844/31) ≅ 9,88.
Luego, observa que la varianza y la desviación típica son menores en el grupo 1, por lo que concluimos que su dispersión es menor.
Espero haberte ayudado.
-
Alexia Varela
el 28/12/16Alguien me podría ayudar con este ejercicio de ecuaciones diferenciales....
Dada la EDO 3y'' - 5cos(2t-1)y' - 4y = g(t), decide razonadamente si la siguiente expresión puede ser solución general:
y(t) = 1/t - Ct^2 - D(t+1) siendo C y D dos constantes arbitrarias.
La respuesta que dio mi profesora es que debido a que no tenemos g(t) no se puede determinar. Pero si derivamos dos veces la expresión de abajo para sustituir y, y' e y'' nos encontramos con:
y''(t) = 2/(t^3) - 2C
Mi duda es, si al derivar dos veces no desaparece la constante no significa que la expresión es incorrecta?
Alexia Varela
el 28/12/16Muchas gracias por la respuesta pero no me refiero a que la derivación sea erróneo.
Mi duda consiste en que las constantes van apareciendo según integramos, entonces si hacemos la operación inversa(derivar) el mismo número de veces,
no deberían desaparecer todas las constantes? Porque supuestamente debemos tener el mismo número de constantes en relación al grado de la EDO.
-
Camila Bascuñan
el 27/12/16Quien me puede ayudar con derivadas...
Se deja caer desde 100 pies de altura un objeto, su altura en el instante t viene dada por la funcion de posicion s=f(t) = -16t^2 + 100, con s medida en pies y t en segundos
1- Encuentre la velocidad media en los siguientes intervalos:
a) [1;1.5]
b)[1;1.1]
2- Hallar la velocidad para el intante t=1
