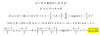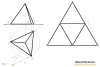
-
Jesus Alvear
el 25/5/19
Para colocar una red en la bahía de una playa se tomaron en la tierra las distancias y el ángulo mostrado en las figura.
1.- ¿Qué longitud tendrá la red para proteger a los bañistas contra ataques de tiburones?
2.- ¿Qué ley se debe aplicar para saber la longitud que tiene la red protectora y cual es su expresión algebraica?
Alejandro
el 25/5/19En princupio con el teorema del coseno: a2=b2+c2-2·b·c·cos(A)
Aunque primero creo tienes que utilizar el del seno: a/sen(A) = b/sen(B) = c/sen(C)
1) 428/sen(78) = 271/sen(B) => B=arcsen{271·sen(78)/248}
2) 360-76-B=A => 360-76-arcsen{271·sen(78)/248}=A
3) a2=2712+4282-2·428·271·cos[B] => a2=2712+4282-2·428·271·cos[360-76-arcsen{271·sen(78)/248}]
-
bb99
el 25/5/19 -
JOSE ANTONIO
el 24/5/19
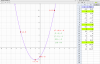
Asunto: 3º eso, funciones Por favor echarme una mano. No sé cómo calcular el apartado b) del ejercicio siguiente. Os adjunto una imagen de la gráfica que he creado en geogebra (GG) y los pasos que he dado. Gracias por anticipado.
Dada la función f(x) = x² + 2x - 3, calcula:
a) f(3), f(-1), f(0) y f(-4). Con esto no he tenido problemas, concretamente f(3) =12, f(-1) = -4, f(0) = -3 y f(-4) = 5.
b) ¿Existe algún valor de x para el que f(x) = a -2?
Observaréis que en la hoja de cálculo de GG ningún valor de y da -2. Con esto creo que podría contestar la pregunta b) pero razonarlo matemáticamente.
-
Vivi
el 24/5/19 -
Carmen Escobar Ruiz
el 24/5/19 -
Carmen Escobar Ruiz
el 24/5/19 -
Carmen Escobar Ruiz
el 24/5/19Hola, alguien me puede ayudar con el siguiente ejercicio, muchas gracias.
Resolver las siguientes operaciones entre los ángulos diedros Â= 65º 35' y
^B= 35º 40'
a. Â + ^B
b. 2Â - 3^BEl apostrofe va encima de la B pero no se ponerlo....
-
Darío
el 24/5/19 -
Pica
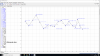
el 24/5/19Buenos dias Unicoos, podrian ayudarme. No he podido comprender esto. Creo que los valores pueden ser ficticios.
-
Guido Ferrari
el 24/5/19
