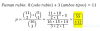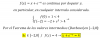-
Hola a todos.
¿Alguien sabría decirme si hay algún vídeo que me pueda ayudar a entender esto? He buscado pero no encuentro nada.
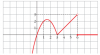
--> Estudia la discontinuidad de la siguiente función según su gráfica:
Adrián Garrido Blanco
el 27/5/19No soy profe ni nada pero creo que eso sé hacerlo.
Debes estudiar la contuniudad de la función, pues te pide que reconozcas en qué valores f(x) no es continua.
En este caso hay una discontinuidad de salto finito en x=6.
Existen tres tipos fundamentales de discontinuidad: salto finito, salto infinito y evitable, unicoos tiene videos sobre ello.
Adrián Garrido Blanco
el 27/5/19 -
Breaking Vlad
el 29/5/19Hola Sergio,
Se trata de que vosotros intentéis resolver los ejercicios por vuestra cuenta, y preguntarnos las dudas concretas que os surjan durante el proceso.
Probabilidad - EBAU 2018 Madrid
Un saludo.
-
Antonio Silvio Palmitano
el 27/5/19Tienes la expresión de la altura del globo en función del tiempo:
f(x) = 64x2 - (1/2)x4 (1),
cuya derivada primera tiene la expresión:
f ' (x) = 128x - 2x3 (2),
y cuya derivada segunda queda expesada:
f '' (x) = 128 - 6x2 (3).
a)
Planteas la condición de posición del globo a nivel del suelo (su altura es igual a cero), y queda la ecuación:
f(x) = 0, sustituyes la expresión señalada (1), y queda:
64x2 - (1/2)x4 = 0, extraes factor común, y queda:
x2(64 - (1/2)x2) =0,
y por anulación de una multiplicación, tienes las opciones:
1°)
x2 = 0, extraes raíz cuadrada en ambos miembros, y queda:
x = 0, que corresponde al instante de partida del globo;
2°)
64 - (1/2)x2 = 0, restas 64 en ambos miembros, y queda:
-(1/2)x2 = -64, multiplicas por -2 en amos miembros, y queda:
x2 = 128, extraes raíz cuadrada positiva en ambos miembros, y queda:
x = √(128) m ≅ 11,314 h, que es el instante en el cuál el globo vuelve a estar a nivel del suelo.
b)
Planteas la condición de altura máxima, y queda la ecuación:
f ' (x) = 0, sustituyes la expresión señalada (2), y queda:
128x - 2x3 = 0, extraes factores comunes, y queda:
2x(64 - x2) = 0,
y por anulación de una multiplicación, tienes las opciones:
1°)
2x = 0, y de aquí despejas:
x = 0, que es el instante de partida del globo;
2°)
64 - x2 = 0, y de aquí despejas:
x = 8 h, evalúas la expresión de la función derivada segunda señalada (3) para este valor, y queda:
f '' (8) = 128 - 6(8)2 = 128 - 384 = -256 < 0,
por lo que tienes que la gráfica de la función altura es cóncava hacia abajo para el valor que hemos determinado, y puedes concluir que el globo alcanza su altura máxima en el instante: t = 8 h,
y que el valor de dicha altura máxima es:
f(8) = 64(8)2 - (1/2)*(8)4 = 4096 - 2048 = 2048 m.
Espero haberte ayudado.
-
Breaking Vlad
el 27/5/19Hola,
se trata de que planteéis vosotros los ejercicios y nos preguntéis dudas concretas. Estamos para ayudaros con la resolución de problemas, no para resolverlos por vosotros.
te recomiendo este vídeo: Función a trozos - Discontinuidad 01
Inténtalo, y coméntanos las dudas que te hayan salido por el camino.
-
Breaking Vlad
el 27/5/19Antonio
el 28/5/19 -
Bueno, debería subir lo que he puesto, pero por ir al grano, lo he intentado por tabla de contingencia, por diagrama de árbol, por probabilidad compuesta... y no llego a resultados coherentes: a lo más coherente que llegué fue que puse la suma de que las 3 sean fumadores y 2 de los 3, dándome 8/16*7/15*6/14+8/16*7/15*8/14, pero no me sale parecido al resultado propuesto.
-
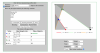
Buenas noches. Alguien me podría resolver este ejercicio por favor? Le estaría eternamente agradecida

Breaking Vlad
el 29/5/19Hola Isabel,
desde unicoos contestamos duda que estén directamente relacionadas con vídeos de la plataforma. Además, se trata de que vosotros intentéis resolver los ejercicios por vuestra cuenta, y preguntarnos las dudas concretas que os surjan durante el proceso.
Un saludo.
-
Hola, a la hora de hacer una integral racional por el método de a y b (puesto que el polinomio de arriba es de menor grado que el de abajo) el resultado cambia dependiendo de a qué parte del polinomio factorizado le asigne a A y la B (cómo se ve en la foto los dos casos posibles), que puedo hacer?

David
el 26/5/19WillProyects
el 27/5/19David
el 27/5/19dentro de un orden y un criterio que tomes, no importa cómo pongas A y B, pero al final deben salir un par de valores, lo que tienes que hacer es operar fracciones con incógnitas en el denominador ("abajo") como siempre lo has hecho de otros cursos. No sé si he aclarado tu duda. Practica más ejemplos (seguro que aquí hay vídeos sobre ello) , y ya verás como salen.